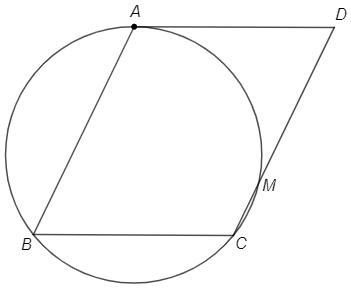
Вершины A, B и C параллелограмма ABCD принадлежат окружности так, что прямая AD касается окружности, а сторона CD пересекает окружность в точке M и делится точкой M в отношении 3:1, считая от вершины D. Найдите сумму квадратов длин диагоналей параллелограмма, если длина стороны BC равна 2 (2 корня из 3)
(2 корня из 3)
Ответы на вопрос
Ответил siestarjoki
3
AD=BC=2√3, AB=DC (противоположные стороны параллелограмма)
DM:MC=3:1
DM=3x, DC=4x
Квадрат касательной равен произведению секущей на ее внешнюю часть.
AD^2 =DC*DM => 12=4x*3x => x=1
DC=4
Сумма квадратов диагоналей параллелограмма равна сумме квадратов четырех сторон.
AC^2 +BD^2 =2(BC^2 +DC^2) =2(12+16) =56
Приложения:
Новые вопросы
Қазақ тiлi,
1 год назад
Математика,
6 лет назад
Алгебра,
6 лет назад
Математика,
8 лет назад
Литература,
8 лет назад