Алгебра, вопрос задал Nurzhan94 , 6 лет назад

вычислите интегралы .........................................

Приложения:

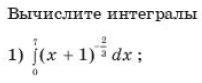
Simba2017: x+1=t

Simba2017: тогда интеграл от степенной функции

Ответы на вопрос

Ответил NNNLLL54

Ответ:

$\displaystyle \int\limits^7_0\, (x+1)^{-\frac{2}{3}}\, dx=\int\limits^7_0\, (x+1)^{-\frac{2}{3}}\, d(x+1)=\frac{(x+1)^{\frac{1}{3}}}{\frac{1}{3}}+C=3\, (x+1)^{\frac{1}{3}}+C=\\\\\\=3\cdot \sqrt[3]{x+1}+C$

Ответил Farhad67

Сначала найдём неопределённый интеграл. Пусть x+1=y :

$\int \: y^{ - \frac{2}{3} }dy= 3 \sqrt[3]{y} = 3 \sqrt[3]{x + 1}$

По формуле Ньютона-Лейбница:

$\int\limits_{a}^{b}{f(x)dx} = F(b)－F(a)$

следовательно:

$\int\limits_{0}^{7}{ {(x + 1)}^{ - \frac{2}{3}} dx} = 3 \sqrt[3]{8} －3 \sqrt[3]{1} = 6-3=3$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

слово объём по составу...

Другие предметы, 1 год назад

Нужно три вопроса про распорядок дня в школе...

Математика, 6 лет назад

98 и 95 номер молю пожалуйста зделайте мне ещё кучу домашки ПОЖАЛУЙСТА!

Математика, 6 лет назад

Помогите пожалуйста очень срочно надо прошу умаляю вас прошу завтра надо здать.

Математика, 8 лет назад

Площадь посева в первый год составила 200гектаров,во второй год её увеличили на 20%,и в третий год-ещё на 20%.Сколько гектаров составила площадь посева в третий год.

Литература, 8 лет назад

Как подписывался Ф.И. Тютчев в "Современнике"?