Алгебра, вопрос задал maria1226 , 2 месяца назад

віддам всі бали допоможіть будь ласка

Приложения:

Ответы на вопрос

Ответил 7x8

1

Знаменник не може дорівнювати 0.

$1)\\g(x)=\frac{3x}{3x^2-2x-5}\\\\3x^{2} - 2x - 5 =0\\\\\ a=3 ,\ \ b=-2 ,\ \ c=-5\\\\ D = b^2 - 4ac = ( - 2)^2 - 4\cdot3\cdot( - 5) = 4 + 60 = 64\\\\\sqrt{D} =\sqrt{64} = 8\\\\ x_1=\frac{-b-\sqrt{D}}{2a}=\frac{2-8}{2\cdot3}=\frac{-6 }{6 }=-1\\\\ x_2=\frac{-b+\sqrt{D}}{2a}=\frac{2+8}{2\cdot3}=\frac{10}{6}= \frac{ 5 }{ 3 }=1\frac{2}{3}$

Відповідь:

$\underline{x\in(-\infty;-1)\cup(-1;1\frac{2}{3})\cup(1\frac{2}{3};+\infty)}$

2)

Під квадратним коренем можна підкладати лише невід’ємні числа.

Знаменник не може дорівнювати 0.

$12-4x > 0\\\\-4x > -12\ \ \ |:(-4)\\\\x < 3$

Відповідь:

$\underline{x\in(-\infty;3)}$

===========================

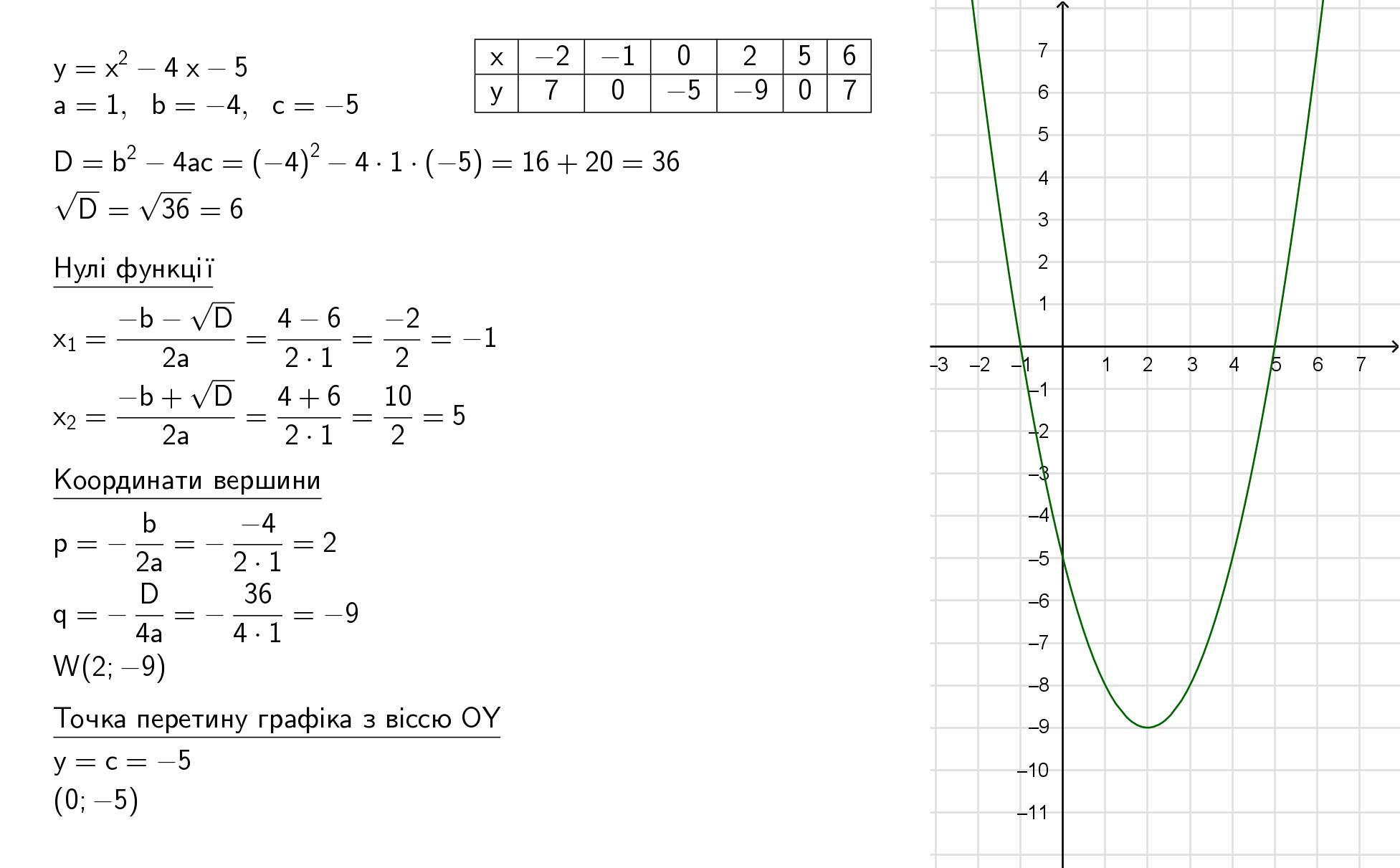
графік на фото

$y=x^2-4x-5$

1) область значень даної функції

$[-9;+\infty)$

2)

проміжок зростання

$[2;+\infty)$

проміжок спадання функції

$(-\infty;2]$

3)

нулі даної функції

$-1;\ 5$

===========================

При яких значеннях в і с точка (-1; 5) є вершиною параболи

$y = 4x^2+ bx+c$

точка N(-1; 5) є вершиною параболи

1. b

Координати вершини

$m=-\frac{b}{2a}\\\\-1=-\frac{b}{2\cdot4}\\\\\frac{b}{8}=1\ \ \ |\cdot 8\\\\b=8$

2. c

Рівняння функції має вигляд

$y = 4x^2+ 8x+c\\\\f(-1)=5\\\\4\cdot(-1)^2+8\cdot(-1)+c=5\\\\4\cdot 1-8+c=5\\\\4-8+c=5\\\\c=5-4+8\\\\c=9$

Відповідь:

$b=8,\ c=9$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 2 месяца назад

Представьте число 2/3 в виде суммы аликвотных дробей двумя способами способами.

Английский язык, 2 месяца назад

срочно помогите !!!!!!!!! Поставьте вместо точек модальные глаголы: Must, Can, May 1. You ... not cross the street when the light is red. 2. He is good sportsman. He ... run and jump well. 3. ... I...

Математика, 2 месяца назад

Сколькими способами можно переставить буквы в слове “ЭКОНОМИКА” так, чтобы гласные буквы всегда были рядом? Где ошибки и что не так?

Математика, 2 месяца назад

16.3найдіть відстань від точки М до площини трикутника АВС, якщо АВ = BC = АС = 5/3 см; MA = MB = MC = = 13 см.

Биология, 6 лет назад

Гипотеза самопроизвольного зарождения жизни: и приведите 2 примера...

Физика, 6 лет назад

на якій висоті тиск атмосфери дорівнює 720мм мм рт ст...