Знайти локальні екстремуми функції.
Приложения:
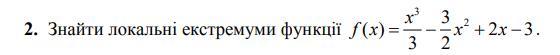
Ответы на вопрос
Ответил pushpull
1
Ответ:
точка х₁ = 2 - точка локального минимума функции.
точка x₂ = 1 - точка локального максимума функции.
Объяснение:
Находим первую производную
Находим стационарные точки (приравниваем производную нулю)
Определяем, где минимум, где максимум
Находим вторую производную
f''(x) = 2x-3
f″(1) = (-1) f''(1) < 0 ⇒ точка x₂ = 1 - точка локального максимума функции.
f″(2) = 1 f″(2) >0 ⇒ точка х₁ = 2 - точка локального минимума функции.
fctdgsygfdhngfxzgsac:
спасибо Вам большое))
Новые вопросы
Русский язык,
11 месяцев назад
Биология,
11 месяцев назад
Математика,
11 месяцев назад
Алгебра,
11 месяцев назад
Математика,
6 лет назад