Математика, вопрос задал buuyy , 1 год назад

Вычислить неопределённый интеграл(с подробным решением)

Приложения:

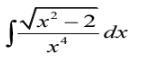
Ответы на вопрос

Ответил axatar

Ответ:

$\frac{1}{6}*\sqrt{(1-\frac{2}{x^{2}} )^{3}} +C$

Пошаговое объяснение:

$\int\limits {\frac{\sqrt{x^{2}-2 } }{x^{4} } } \, dx =\int\limits {\sqrt{\frac{x^{2}-2 }{x^{2} } } *x^{-3} } \, dx =\int\limits {\sqrt{1-\frac{2}{x^{2} } } * (-\frac{1}{2} )} \, d(x^{-2} ) =\\\\=\int\limits {\sqrt{1-2*x^{-2}} } * \frac{1}{4} } \, d(-2*x^{-2} ) =\\\\=\frac{1}{4}*\int\limits {(1-2*x^{-2})^{\frac{1}{2} } } } \, d(1-2*x^{-2} ) =\\$

$=\frac{1}{4}*\frac{(1-2*x^{-2})^{\frac{1}{2} +1} }{\frac{1}{2} +1} +C =\frac{1}{4}*\frac{(1-2*x^{-2})^{\frac{3}{2} } }{\frac{3}{2}} +C =\\\\=\frac{1}{4}*\frac{2}{3}*(1-2*x^{-2})^{\frac{3}{2} }+C=\frac{1}{6}*\sqrt{(1-\frac{2}{x^{2}} )^{3}} +C$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Қазақ тiлi, 1 год назад

Пожалуйста срочно помогите страница 150 № 2 казахский язык 4 класс 2 часть...

Английский язык, 1 год назад

before i came back home my little brother clean the room записать в Past Perfect...

Физика, 1 год назад

Если растягивать пружину 10н её длина =12см если расстягивать пружину 30н её длина =20см какова длина недиформированой длины...

Геометрия, 1 год назад

На дворе была сделана цветочная клумба, образованная из квадрата и четырёх полукругов. Площадь клумбы приблизительно равна 90 м². Сколько метров декоративного забора необходимо вокруг клумбы? В...

История, 6 лет назад

ПРОДЕМОНСТРИРУЙТЕ НА ПРИМЕРАХ, что принятие идеологии Просвещения было в интересах европейских монархов.

Алгебра, 6 лет назад

помогите решить срочно ...