Всё еще надеюсь на вас, знатоки стереометрии! Помогите!
Приложения:

Ответы на вопрос
Ответил Andr1806
0
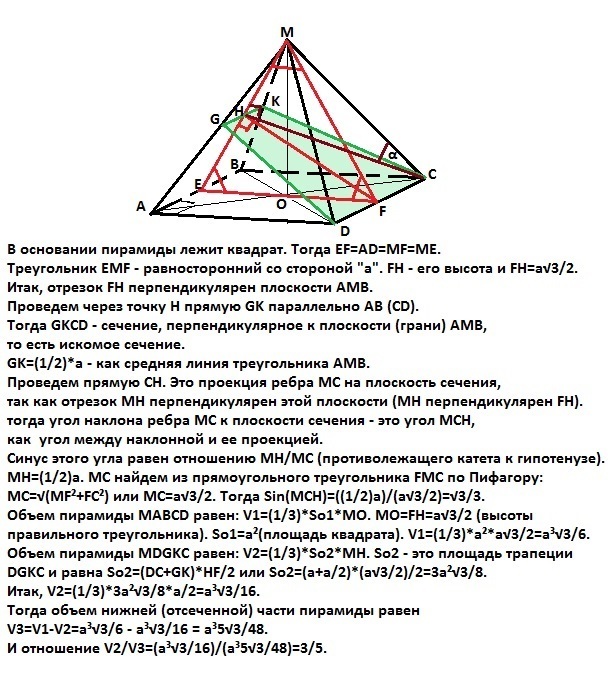
В основании пирамиды лежит квадрат.
Тогда EF=AD=MF=ME.
Треугольник EMF - равносторонний со стороной "а".
FH - его высота и FH=a√3/2.
Итак, отрезок FH перпендикулярен плоскости АМВ.
Проведем через точку Н прямую GK параллельно АВ (СD).
Тогда GKCD - сечение, перпендикулярное к плоскости (грани) АМВ,
то есть искомое сечение.
GK=(1/2)*a - как средняя линия треугольника АМВ.
Проведем прямую СН. Это проекция ребра МС на плоскость сечения,
так как отрезок МН перпендикулярен этой плоскости (МН перпендикулярен FH).
тогда угол наклона ребра МС к плоскости сечения - это угол МСН,
как угол между наклонной и ее проекцией.
Синус этого угла равен отношению МН/МС (противолежащего катета к гипотенузе).
МН=(1/2)а. МС найдем из прямоугольного треугольника FMC по Пифагору:
МС=√(МF²+FC²) или МС=а√3/2.
Тогда Sin(MCH)=((1/2)а)/(а√3/2)=√3/3.
Объем пирамиды МАВСD равен:
V1=(1/3)*So1*MO. МО=FH=a√3/2 (высоты правильного треугольника).
So1=a²(площадь квадрата).
V1=(1/3)*a²*a√3/2=a³√3/6.
Объем пирамиды МDGKC равен:
V2=(1/3)*So2*MH. So2 - это площадь трапеции DGKC и равна
So2=(DC+GK)*НF/2 или So2=(а+а/2)*(а√3/2)/2=3a²√3/8.
Итак, V2=(1/3)*3a²√3/8*а/2=a³√3/16.
Тогда объем нижней (отсеченной) части пирамиды равен
V3=V1-V2=a³√3/6 - a³√3/16 = a³5√3/48.
И отношение V2/V3=(a³√3/16)/(a³5√3/48)=3/5.
Тогда EF=AD=MF=ME.
Треугольник EMF - равносторонний со стороной "а".
FH - его высота и FH=a√3/2.
Итак, отрезок FH перпендикулярен плоскости АМВ.
Проведем через точку Н прямую GK параллельно АВ (СD).
Тогда GKCD - сечение, перпендикулярное к плоскости (грани) АМВ,
то есть искомое сечение.
GK=(1/2)*a - как средняя линия треугольника АМВ.
Проведем прямую СН. Это проекция ребра МС на плоскость сечения,
так как отрезок МН перпендикулярен этой плоскости (МН перпендикулярен FH).
тогда угол наклона ребра МС к плоскости сечения - это угол МСН,
как угол между наклонной и ее проекцией.
Синус этого угла равен отношению МН/МС (противолежащего катета к гипотенузе).
МН=(1/2)а. МС найдем из прямоугольного треугольника FMC по Пифагору:
МС=√(МF²+FC²) или МС=а√3/2.
Тогда Sin(MCH)=((1/2)а)/(а√3/2)=√3/3.
Объем пирамиды МАВСD равен:
V1=(1/3)*So1*MO. МО=FH=a√3/2 (высоты правильного треугольника).
So1=a²(площадь квадрата).
V1=(1/3)*a²*a√3/2=a³√3/6.
Объем пирамиды МDGKC равен:
V2=(1/3)*So2*MH. So2 - это площадь трапеции DGKC и равна
So2=(DC+GK)*НF/2 или So2=(а+а/2)*(а√3/2)/2=3a²√3/8.
Итак, V2=(1/3)*3a²√3/8*а/2=a³√3/16.
Тогда объем нижней (отсеченной) части пирамиды равен
V3=V1-V2=a³√3/6 - a³√3/16 = a³5√3/48.
И отношение V2/V3=(a³√3/16)/(a³5√3/48)=3/5.
Приложения:
Новые вопросы
История,
2 года назад
Английский язык,
2 года назад
Физика,
8 лет назад
Геометрия,
8 лет назад
Математика,
9 лет назад