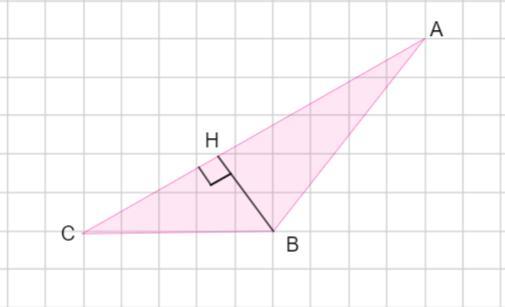
Геометрия, вопрос задал morozzena32 , 1 год назад

У трикутнику ABC R = 8,125 см,cos B = -5\13 ,cos C= 0,6 . Знайдіть периметр трикутника і найменшу його висоту.

Ответы на вопрос

Ответил lilyatomach

Ответ:

Периметр треугольника 32 см, а меньшая высота 3,2 см.

Объяснение:

В треугольнике АВС R= 8,125 см, cosB = -5/13, cos C =0,6. Найти периметр и наименьшую его высоту .

Пусть дан Δ АВС , так как cosB отрицательное число, то этот угол тупой и треугольник тупоугольный.

Воспользуемся основным тригонометрическим тождеством и найдем синусы данных углов.

$sin^{2} B +cos^{2} B=1;\\sin^{2} B =1- cos^{2} B;\\\\sin^{2} B=1-\left (-\dfrac{5}{13}\right )^{2} =1- \dfrac{25}{169} =\dfrac{169}{169} -\dfrac{25}{169} =\dfrac{144}{169} ;\\\\sinB =\dfrac{12}{13}$

$sin^{2} C +cos^{2}C=1;\\sin^{2} C =1- cos^{2}C;\\\\sin^{2}C=1-(0,6)^{2} =1-0,36=0,64;\\sinC =\sqrt{0,64} =0,8$

Воспользуемся следствием из теоремы синусов

$\dfrac{AB}{sinC} =\dfrac{AC}{sinB} =\dfrac{BC}{sinA} =2R$

Так как по условию R= 8,125 см, то 2R= 16,25 см

Тогда

$\dfrac{AB}{0,8} =16,25;\\\\AB =16,25\cdot 0,8=13$ см

$\dfrac{AC}{sinB} =2R\\\\AC = 16,25 \cdot \dfrac{12}{13} = 16\dfrac{1}{4} \cdot \dfrac{12}{13} = \dfrac{65}{4} \cdot \dfrac{12}{13} =\dfrac{13\cdot5\cdot 4\cdot3}{4\cdot13} =15$ см.

Найдем синус угла А . Сумма углов треугольника равна 180°.

Тогда ∠ А = 180° - (∠В+∠С)

sinA =sin( 180° - (∠В+∠С) ) =sin (∠В+∠С)=sinB·cosC +cos B ·sin C ;

$sin A = \dfrac{12}{13} \cdot 0,6 +\left(- \dfrac{5}{13}\right )\cdot 0,8= \dfrac{12}{13} \cdot \dfrac{6}{10} - \dfrac{5}{13} \cdot \dfrac{8}{10} =\dfrac{72}{130}- \dfrac{40}{130} =\dfrac{32}{130} =\dfrac{16}{65}.$

$\dfrac{BC}{sinA} =2R;\\\\BC = 2R \cdot sinA;\\\\BC =16,25\cdot \dfrac{16}{65} =16\dfrac{1}{4} \cdot \dfrac{16}{65} =\dfrac{65}{4} \cdot\dfrac{16}{65} =4$ см.