Тригонометрия решить уравнение
Приложения:
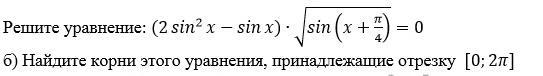
Ответы на вопрос
Ответил Miroslava227
1
Ответ:
ОДЗ:
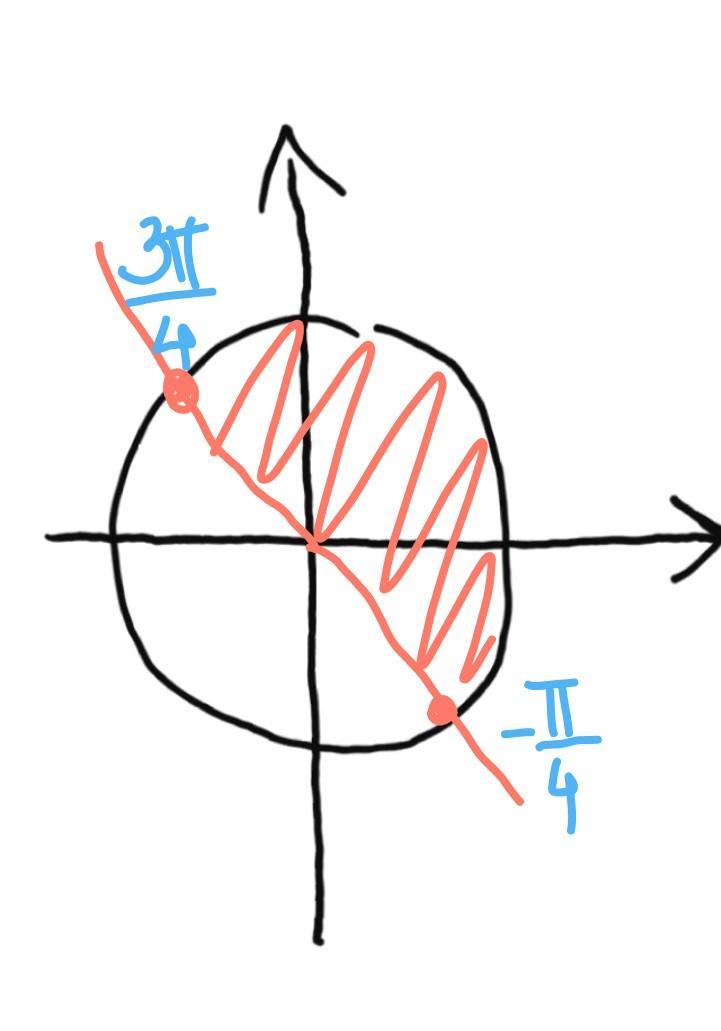
рисунок
n принадлежит Z.
корень х3 не входит в ОДЗ
корень х5 не входит ОДЗ.
В итоге получаем:
n принадлежит Z.
б)
[0;2П]
Приложения:
mrakobes95:
Круто. Спасибо
Новые вопросы
Английский язык,
1 год назад
Русский язык,
1 год назад
Алгебра,
2 года назад
Русский язык,
2 года назад
Математика,
8 лет назад
Алгебра,
8 лет назад