Сторона AC в треугольнике ABC равна 10 и BC=2* AB.
Найти длину медианы BM , если известно, что расстояние от точки
Aдо прямой BM равно 4.
Ответы на вопрос
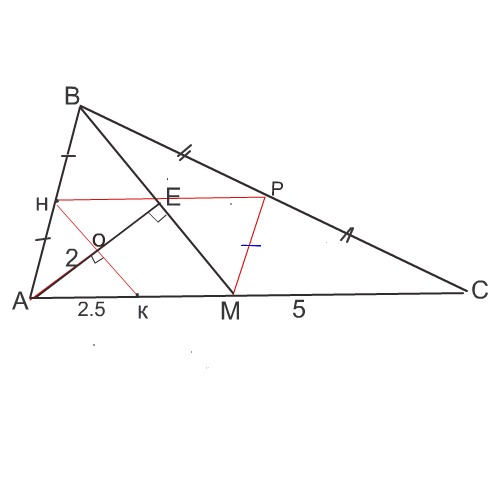
Сделаем рисунок к задаче, стараясь придерживаться заданных в ней пропорций.
Обозначим середины АВ и ВС как Н и Р соответственно. Проведем отрезок НР - среднюю линию треугольника АВС.
Обозначим точку К - середину АМ.
Соединим середины АВ и АМ отрезком НК.
НК параллельна ВМ как средняя линия треугольника АВМ и, соответственно, равна половине медианы ВМ.
Рассмотрим треугольник АКО. В нем АО перпендикулярна КН, т.к. АЕ - расстояние от А до ВМ определяется отрезком, перпендикулярным ВМ.
Поскольку КН параллельна ВМ, то АО перпендикулярна КН.
Из треугольника АОК, в котором АО=половине АЕ, а АК - половине АМ,
по теореме Пифагора найдем ОК.
ОК=√(2,5²-2²)=1,5 см
КН=2 ОК=3 см
ВМ=2КН=6 см