СРОЧНО!!!!!
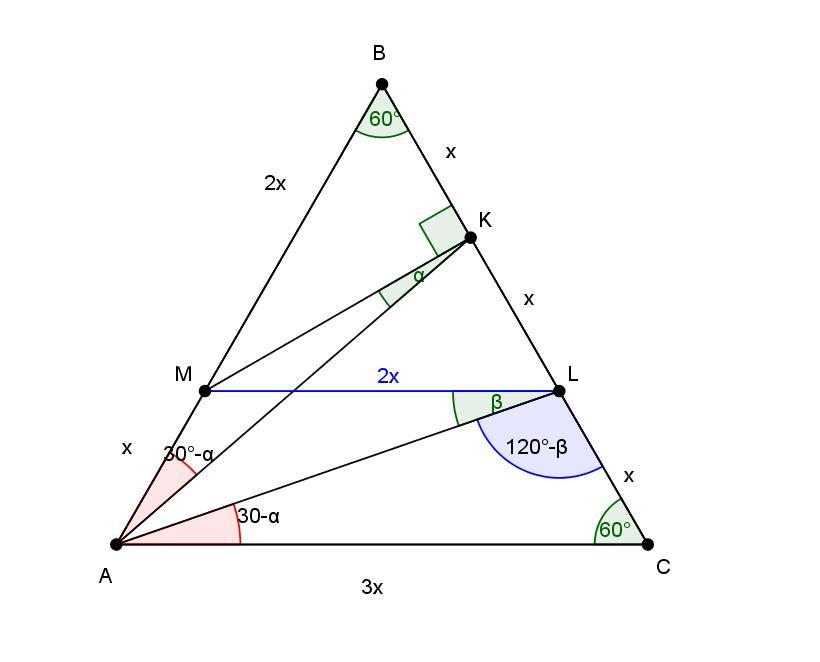
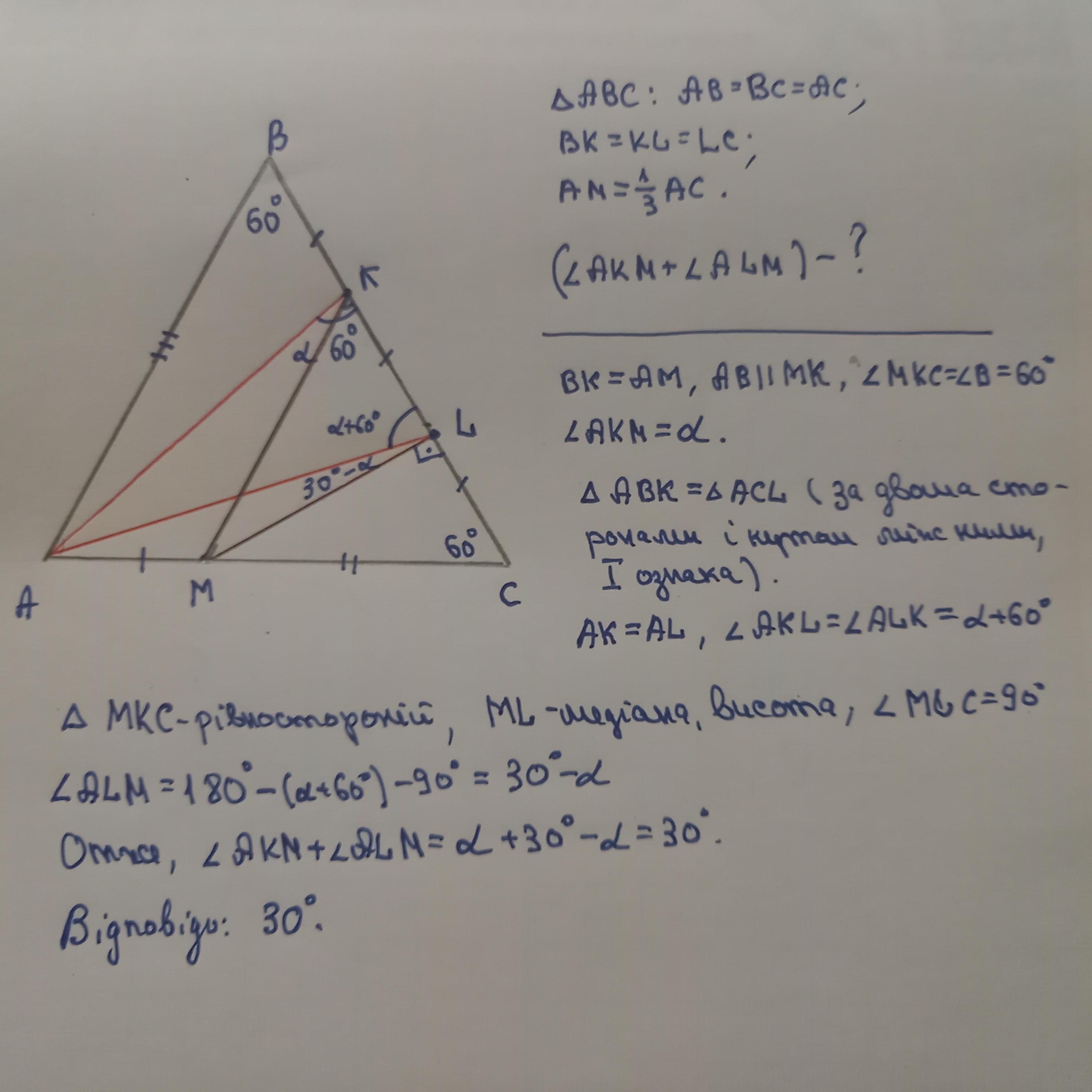
На стороне BC равностороннего треугольника ABC отмечены точки K и L так, что BK=KL=LC, а на стороне AC отмечена точка M так, что AM=AC/3. Найдите сумму углов AKM и ALM.
Ответы на вопрос
Ответил 7x8
2
Ответ:
∠AKM +∠ ALM=30°
Пошаговое объяснение:
1. AMLC
AM=LC - AMLC равнобедренная трапеция
∠AML=∠MLC=180°-60°=120°
∠ALC=∠MLC-∠MLA
∠ALC=120°-β
2. ΔMBL
MB=2x
BL=2x
∠MBL=60°
ΔLMB - равносторонний треугольник
BK=KL=x так МК это высота
∠BKM=90°
3. ΔABK
∠BKA=90°+α
Сумма внутренних углов треугольника равна 180°.
∠ABK+∠BKA+∠BAK=180°
60°+90°+α+∠BAK=180°
∠BAK=180°-60°-90°-α
∠BAK=30°-α
4. ΔALC
AC=3x=AB
LC=x=BK
∠ACL=60°=∠ABK
ΔALC и ΔABK конгруэнтные треугольники
∠LAC=∠BAK=30°-α
∠LAC+∠ALC+∠LCA=180°
30°-α+120°-β+60°=180°
-α-β=180°-30°-120°-60°
-α-β=-30° |:(-1)
α+β=30°
Приложения:
Ответил aarr04594
1
30°
####################
Приложения:
Новые вопросы