Алгебра, вопрос задал selfcare39 , 10 месяцев назад

СРОЧНО ДАЮ 100б Найдите производную сложных функций

Приложения:

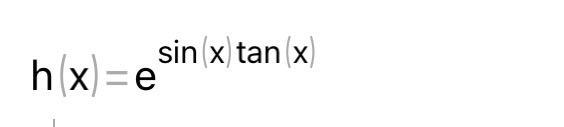
Ответы на вопрос

Ответил pushpull

1

Ответ:

$\displaystyle h'(x) = \bigg(sin(x)+\frac{sin(x)}{cos^(x)} \bigg)*e^{sin(x)*tg(x)}$

Объяснение:

$\displaystyle h(x) = e^{sin(x)*tg(x)}\\\\\\h'(x) = \bigg(e^{sin(x)*tg(x)}\bigg)'*\bigg(sin(x)*tg(x)\bigg)'\\\\\\ \bigg(e^{sin(x)*tg(x)}\bigg)' = e^{sin(x)*tg(x)}\\\\\\(uv)'=u'v+uv'\\\\\bigg(sin(x)*tg(x)\bigg)'= (sin(x))'*tg(x)+sin(x)*(tg(x))'=\\\\\\=cos(x)*tg(x)+sin(x)*\frac{1}{cos^2(x)}$

ответ

$\displaystyle h'(x) = \bigg(sin(x)+\frac{sin(x)}{cos^(x)} \bigg)*e^{sin(x)*tg(x)}$

selfcare39: Помогите пожалуйста с еще одним заданием задание у меня в профиле

pushpull: сделала

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Физика, 6 месяцев назад

5 Определите постоянную дифракционной решетки, если при ее освещении светом с дли- ной волны 620 нм спектр второго порядка виден под углом 15. (sin150 = 0,2588) Сколько штрихов на мм имеет данная...

Алгебра, 6 месяцев назад

построить график функции у= -х² у= х² Определите свойства... сроочнооооо...

Химия, 10 месяцев назад

э. Определите правдивость утверждений и внесите ответы в таблицу в форме правда/ложь Правда/ложь №o Утверждения 1 В промышленности водород получают электролизом из воды В лабораторных условиях...

Алгебра, 10 месяцев назад

Помогите пожалуйста решить дам 100 баллов $\sqrt{2(x^{2} -6x)+19}+\sqrt{{3(x^{2} -6x)+36}}=-2x^{2} +12x-14$ ...

Алгебра, 6 лет назад

пожалуйста,очень надо...

Английский язык, 6 лет назад

True (+) or false (-)? CORRECT the false statements! a) Paul studies at the university. b) Paul gets up at 8.30 on working days. c) Paul has breakfast with his family. d) It takes him 5-10...