Срочно!! 40 баллов
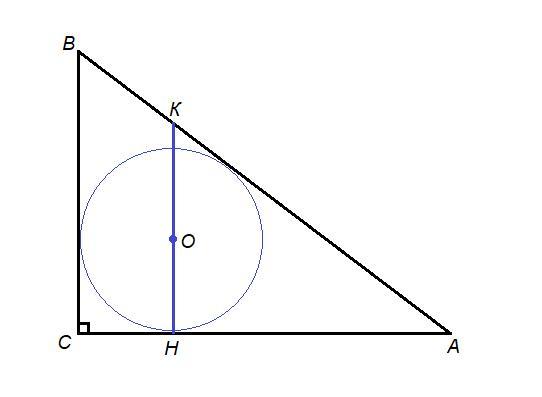
У трикутника ABC кут C=90 градусiв, BC=3 см,AC=4 см. Точка дотику вписаного кола поділяє більший катет на відрізки 1 і 3 см, рахуючи від вершини прямого кута. Через центр вписаного кола проведено пряму паралельно катету BC. Знайдіть довжину відрізка цієї прямої, що лежить між сторонами AB і AC
Ответы на вопрос
Ответил KuOV
4
Ответ:
KH = 2,25 см
Объяснение:
Пусть Н точка касания вписанной окружности с катетом АС.
СН = 1 см, НА = 3 см.
Свойство касательной:
- Радиус, проведенный в точку касания, перпендикулярен касательной.
Проведем радиус ОН в точку касания.
ОН⊥АС по свойству касательной,
ВС⊥АС как катеты, значит ОН║ВС как перпендикуляры к одной прямой.
Продлим ОН до пересечения с гипотенузой АВ в точке К.
КН - искомый отрезок.
ΔAKH ~ ΔABC по двум углам:
∠А - общий,
∠АНК = ∠АСВ = 90°.
Из подобия треугольников следует:
KH = 2,25 см
Приложения:
familypaterandrei200:
Спасибо!
Новые вопросы