Алгебра, вопрос задал raminamamaseitova , 1 год назад

Составьте квадратное уровнение по его корням
( По Теореме Виета ) ДАЮ 40 БАЛЛОВ ВСЕГО НУЖНО 2 УРОВНЕНИЯ

Приложения:

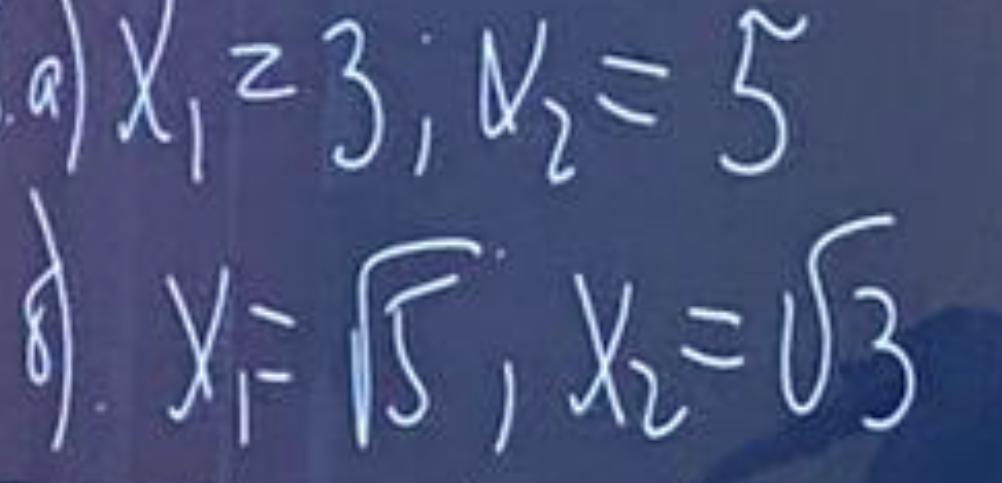
Ответы на вопрос

Ответил NNNLLL54

Ответ:

Если известны корни квадратного уравнения $\bf x^2+px+q=0$ , то можно написать уравнение, применив теорему Виета .

$\bf x_1\cdot x_2=q\ \ ,\ \ x_1+x_2=-p$ .

$\bf a)\ \ x_1=3\ ,\ x_2=5\\\\x_1\cdot x_2=15\ \ ,\ \ x_1+x_2=8\\\\q=15\ \ ,\ \ p=-8\\\\x^2-8x+15=0\\\\\\b)\ \ x_1=\sqrt5\ ,\ x_2=\sqrt3\\\\x_1\cdot x_2=\sqrt{15}\ \ ,\ \ x_1+x_2=\sqrt5+\sqrt3\\\\q=\sqrt{15}\ \ ,\ \ p=-(\sqrt5+\sqrt3)\\\\x^2-(\sqrt5+\sqrt3)\, x+\sqrt{15}=0$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 1 год назад

Рівняння з двома змінними методом Підстановки, Графічного та додавання. Рівняння: 5х+3у=5 ; 2х+у=3. Обов'язково з розписом. Та не обов'язково українською...

Геометрия, 1 год назад

ДАЮ 27 БАЛЛОВ!! Точка дотику вписаного в рівнобедрений трикутник кола ді- лить його бічну сторону на відрізки, різниця яких дорівнює 1 см (менший відрізок прилеглий до кута при основі). Знайдіть...

Математика, 1 год назад

5класс срочно! Площадь прямоугольника 5/7 м². Длинна одной стороны 3/4 м. Найдем длину другой стороны. если что где числа через черту / это дробь в задании ошибок нет!

Физика, 1 год назад

Адиабаталық ұлғаю кезінде газ 400 дж жұмыс жасады, оның ішкі энергиясы қалай және қаншаға өзгереді. Комектесіңдерші өтініш. Срочнооо...

Математика, 6 лет назад

СРООЧНО ПООМОЖІТЬ БУДЬ ЛАСКА...

Биология, 6 лет назад

Как у вас прошла мутация голоса? 3-5 предложений. Написать симптомы.

Составьте квадратное уровнение по его корням ( По Теореме Виета ) ДАЮ 40 БАЛЛОВ ВСЕГО НУЖНО 2 УРОВНЕНИЯ

Ответы на вопрос

Составьте квадратное уровнение по его корням
( По Теореме Виета ) ДАЮ 40 БАЛЛОВ ВСЕГО НУЖНО 2 УРОВНЕНИЯ