Геометрия, вопрос задал школьникИЗроссии , 2 года назад

So-высота конуса
Найдите
1)радиус основания конуса
2)высоту конуса
3)площадь поверхности конуса

Приложения:

Roxandi: Если рассмотреть треугольник SCB, станет ясно, что он равнобедренный, поэтому углы при основании (180-120)/2=30. Дальше треугольник SOB, угол треугольник прямоугольный, поэтому против угла в 30 градусов лежит сторона в половину гипотенузы, h=18/2. Радиус основания можно найти по теореме Пифагора b²=c²-a² (a, b- катеты, c - гипотенуза, c =18, a=h). Площадь всей поверхности конуса - πr(r+l). L - образующая.

Ответы на вопрос

Ответил lilyatomach

Ответ:

H= 9 ед., R=9√3 ед., S= 81 π√3(2+√3) кв. ед.

Объяснение:

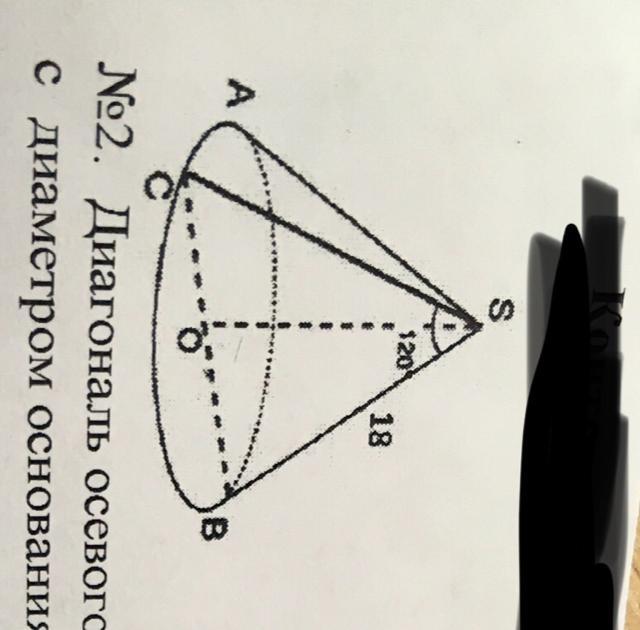
Рассмотрим заданный рисунок.

Δ SCB - осевое сечение конуса.

Δ SCB - равнобедренный треугольник, в котором SB=SC=18 ед., ∠CSB=120°.

SO- высота равнобедренного треугольника, проведенная к основания. Тогда эта высота является медианой и биссектрисой.

∠CSO=∠BSO=60°.

Рассмотрим Δ SOC - прямоугольный.

Так как сумма острых углов прямоугольного треугольника равна 90°,то ∠SCO=90°-60°=30°.

SC=18 ед.

По свойству катета, лежащего напротив угла в 30°

$SO=\dfrac{1}{2} SC;\\SO=\dfrac{1}{2} \cdot18=9$

Значит, высота конуса равна 9 ед.

По теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Тогда

$CO^{2} =SC^{2} -SO^{2};\\CO=\sqrt{SC^{2} -SO^{2}} ;\\CO=\sqrt{18^{2} -9^{2} } =\sqrt{(18-9)(18+9)} =\sqrt{9\cdot27} =3\sqrt{9\cdot3} =9\sqrt{3}$

Тогда радиус основания конуса равен 9√3 ед.

Найдем площадь поверхности конуса. Она состоит из боковой поверхности и площади основания.

$S=\pi Rl+\pi R^{2} ,$

где R-радиус основания конуса ,l - образующая конуса.

$S=\pi \cdot9\sqrt{3} \cdot 18+\pi \cdot(9\sqrt{3} )^{2} =\pi\cdot 9\sqrt{3} (18+9\sqrt{3} )=\pi\cdot 9\sqrt{3}\cdot9 (2+\sqrt{3} )=\\81\pi \sqrt{3} (2+\sqrt{3} )$