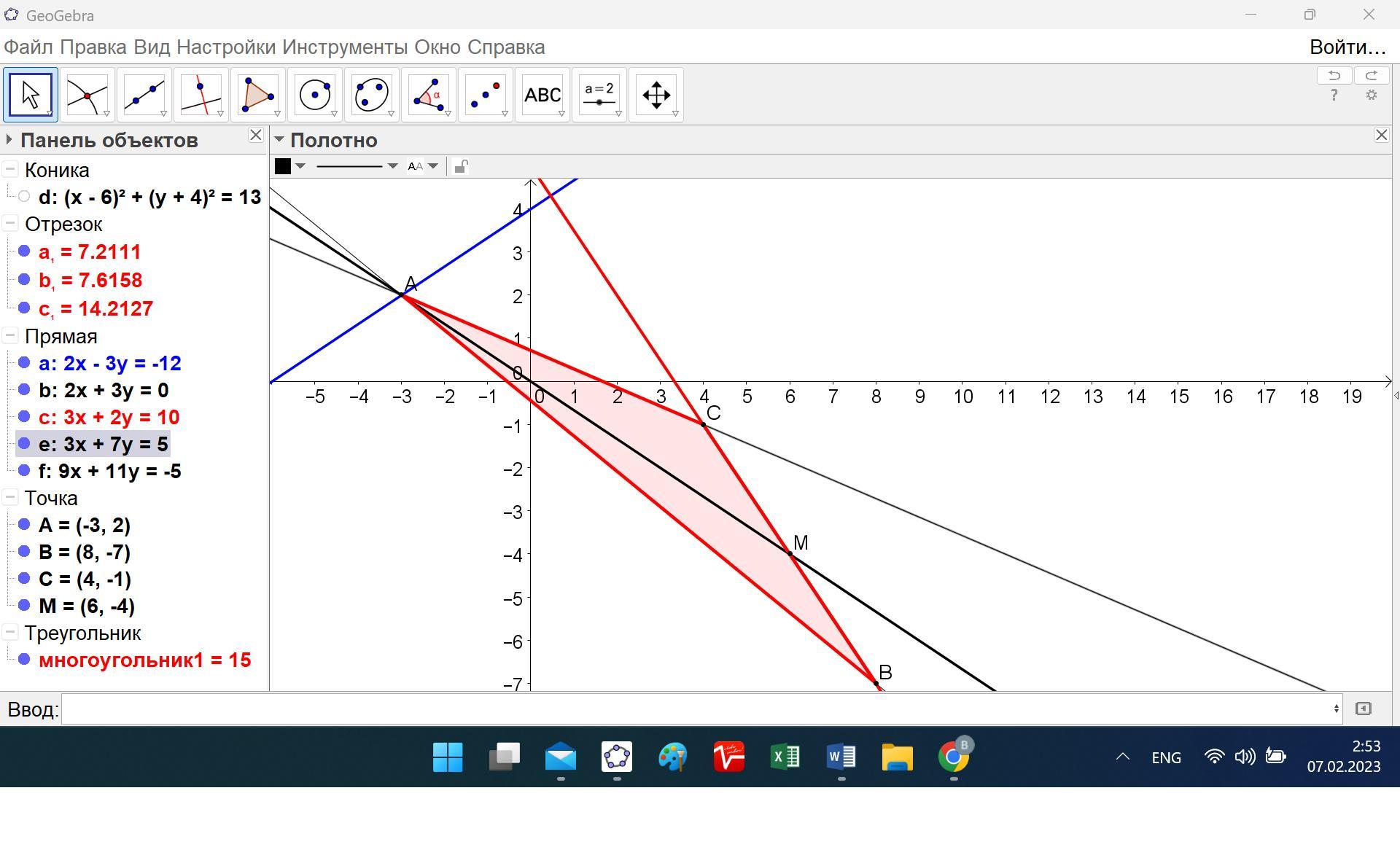
Сложить уравнение сторон треугольника , если известна одна из его вершин C(4;-1) , а также уравнение высоты 2x - 3y +12 = 0 и медианы 2x+3y = 0 , что проведены с одной вершины.

Сложить уравнение сторон треугольника , если известна одна из его вершин C(4;-1) , а также уравнение высоты 2x - 3y +12 = 0 и медианы 2x + 3y = 0 , что проведены с одной вершины.

Находим координаты вершины А, из которой проведены высота и медиана, как точку пересечения заданных прямых.

2x - 3y +12 = 0

2x+3y = 0                

4x +12 = 0,

x = -12/4 = -3.

y = -2x/3 = -2*(-3)/3 = 2.

Найдена точка А(-3; 2).

Можно найти уравнение стороны АС по координатам А(-3; 2) и С(4; -1).

Воспользуемся формулой канонического уравнения прямой:

(x – xa)/(xb – xa) = (y – ya)/(yb – ya)

Подставим в формулу координаты точек:

(x - (-3))/(4 - (-3)) = (y – 2)/((-1) – 2).

В итоге получено каноническое уравнение прямой:

(x + 3)/7 =(y – 2)/(-3).

Из уравнения прямой в каноническом виде получим уравнение прямой общего вида Ах + Ву + С = 0.

-3х – 9 = 7у – 14,

3х + 7у – 5 = 0,

и с угловым коэффициентом:

y = (-3/7)x + (5/7).

Уравнение стороны ВС найдём как перпендикуляр, проходящий через точку С к заданной высоте 2x - 3y +12 = 0.

У перпендикулярной прямой в общем виде коэффициенты А и В меняются на (-В) и А , или на В и (-А).

Получаем ВС: 3х + 2у + С = 0.

Подставим координаты точки С(4; -1).

3*4 + 2*(-1) + С = 0, отсюда С = -12 + 2 = -10.

Уравнение ВС: 3х + 2у - 10 = 0.

Находим координаты точки М (это основание медианы) как точку пересечения стороны ВС 3х + 2у - 10 = 0 и медианы 2x + 3y = 0.

3х + 2у - 10 = 0,  х2 =       6х + 4у - 20 = 0

2x + 3y = 0,         х(-3) = - 6x - 9y = 0        

                                              - 5у – 20 = 0, у = 20/(-5) = -4.

х = -3у/2 = -3*(-4)/2 = 6.

Точка М(6; -4).

Координаты вершины В находим как точку, симметричную точке С(4; -1) относительно точки М.

х(В) = 2х(М) – х(С) = 2*6 – 4 = 8,

y(В) = 2y(М) – y(С) = 2*(-4) – (-1)  =-7.

Точка В(8; -7).

Получаем уравнение стороны АВ.

Подставим в формулу координаты точек:

(x - (-3))/(8 - (-3)) = (y - 2)/((-7) – 2)

В итоге получено каноническое уравнение прямой:

(x + 3)/11 = (y – 2)/(-9).

Из уравнения прямой в каноническом виде получим уравнение

общего вида:

-9х – 27 = 11у – 22,

9х + 11у + 5 = 0,

и с угловым коэффициентом:

y = (-9/11)x – (5/11).