Алгебра, вопрос задал hapfld , 1 год назад

Обчисліть інтеграл, що додається на фото ……….

Приложения:

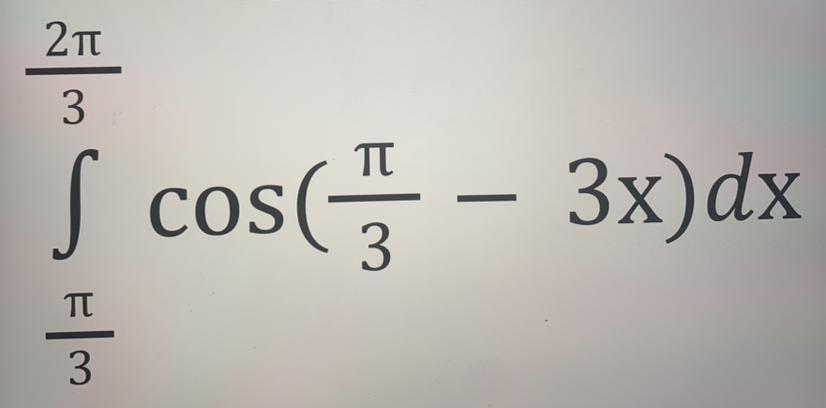
Ответы на вопрос

Ответил mathkot

Ответ:

$\boldsymbol{\boxed{ \int\limits^{\dfrac{2\pi}{3}}_{\dfrac{\pi}{3}} {\cos \bigg (\frac{\pi}{3} - 3x \bigg )} \, dx =-\frac{\sqrt{3} }{3}}}$

Примечание:

По таблице интегралов:

$\boxed{\int {\cos x} \, dx =\sin x+C }$

По свойствам интегралов:

$\boxed{ \displaystyle \int \sum\limits_{i=1}^n {C_{i}f_{i}(x)} \, dx = \sum\limits_{i=1}^nC_{i} \int {f_{i}(x)} \, dx}$

Объяснение:

$\displaystyle \int\limits^{\dfrac{2\pi}{3}}_{\dfrac{\pi}{3}} {\cos \bigg (\frac{\pi}{3} - 3x \bigg )} \, dx = -\frac{1}{3} \int\limits^{\dfrac{2\pi}{3}}_{\dfrac{\pi}{3}} {\cos \bigg (\frac{\pi}{3} - 3x \bigg )} \, d \bigg (\frac{\pi}{3} - 3x \bigg )=$

$\displaystyle = -\frac{1}{3} \cdot \sin \bigg (\frac{\pi}{3} - 3x \bigg ) \Bigg|_{\dfrac{\pi}{3}}^{\dfrac{2\pi}{3}} =-\frac{1}{3} \Bigg (\sin \bigg (\frac{\pi}{3} - 3 \cdot \dfrac{2\pi}{3} \bigg ) - \sin \bigg (\frac{\pi}{3} - 3 \cdot \dfrac{\pi}{3} \bigg ) \Bigg) =$

$\displaystyle =-\frac{1}{3} \Bigg (\sin \bigg (\frac{\pi}{3} - 2\pi \bigg ) - \sin \bigg (\frac{\pi}{3} - \pi \bigg ) \Bigg) =-\frac{1}{3} \Bigg (\sin \bigg (\frac{\pi}{3} \bigg ) +\sin \bigg (\pi - \frac{\pi}{3} \bigg ) \Bigg) =$

$\displaystyle =-\frac{1}{3} \Bigg (\sin \bigg (\frac{\pi}{3} \bigg ) +\sin \bigg ( \frac{\pi}{3} \bigg ) \Bigg) = -\frac{2}{3}\sin \bigg (\frac{\pi}{3} \bigg ) = -\frac{2}{3} \cdot \frac{\sqrt{3} }{2} = -\frac{\sqrt{3} }{3}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Литература, 1 год назад

написати рекламу виду мистецтва (за вибором) Це дуже важливо допоможіть будь ласка!!!!!!!

Алгебра, 1 год назад

Здравствуйте ! Такой вот вопрос ,перед которым я оказался бессилен : "В магазин привезли 3 ящика яблок. В первом и втором ящиках-43кг яблок,во вотором и третьем -55 кг,а в первом и третьем ящиках...

Математика, 1 год назад

Перевір чи правильна пропорція 12:72=6:36...

Биология, 1 год назад

ДАЮ 70 БАЛЛОВ!!! 1. У людини ген полідактилії (шестипалість) домінує над нормальною будовою кисті. Жінка, яка має нормальну кисть, проте її батько шестипалий, вийшла заміж за чоловіка, який має...

Биология, 6 лет назад

... - из других веществ, вошедших в организм из внешней среды, мы Говорим, что в его клетках образуются специфические вещества. Выберите ответ: Энтальпия Одиссимиляция Экзотермия Ассисмиляция...

Русский язык, 6 лет назад

упр.64 помогите пожалуйста. (за ответы точками, на вас идет жалоба. вас блокируют) ...