Скільки нулів має функція g(x) = x(x^2 -4) корінь |х| - 3
Приложения:
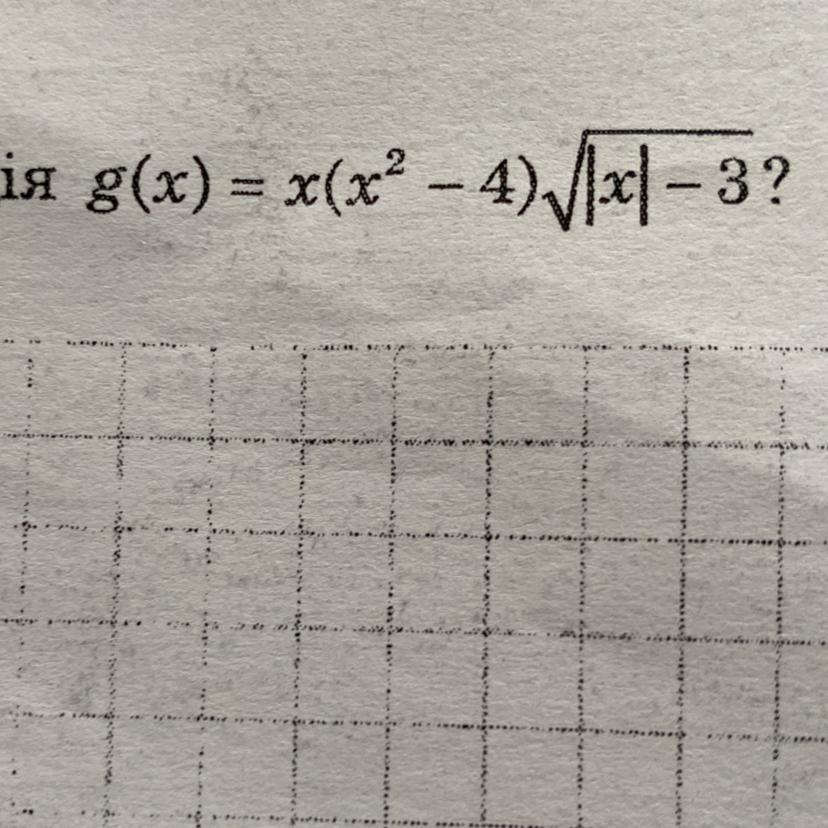
Ответы на вопрос
Ответил ZakharTeshukov
0
Ответ:
Функція g(x) = x(x^2 - 4) корінь |х| - 3 може мати нулі тільки тоді, коли вона дорівнює нулю. Тобто ми повинні розв'язати рівняння:
x(x^2 - 4) корінь |х| - 3 = 0
Розділимо це рівняння на складники:
x = 0 або (x^2 - 4) корінь |х| - 3 = 0
Якщо x = 0, то функція g(x) буде дорівнювати нулю.
Якщо (x^2 - 4) корінь |х| - 3 = 0, то потрібно розв'язати рівняння (x^2 - 4) корінь |х| = 3.
Якщо x = 0, то функція буде дорівнювати нулю. Інакше, якщо x не дорівнює нулю, то корені x^2 - 4 та |х| повинні бути додатніми. Так як корінь |х| завжди не менше 0, то корінь x^2 - 4 повинен бути рівний 3.
Отже, ми маємо розв'язати рівняння x^2 - 4 = 9. Звідси ми знаходимо, що x = -3 або x = 3.
Отже, функція g(x) може мати два нулі: x = 0, x = -3 або x = 3.
Объяснение:
Новые вопросы
Алгебра,
1 год назад
Биология,
1 год назад
Геометрия,
1 год назад
Математика,
1 год назад
Алгебра,
6 лет назад