Доведіть,що коли сторони многокутника,вписаного в коло,рівні,то й усі його кути теж рівні

Ответ:

Доведено, що коли сторони многокутника,вписаного в коло, рівні, то й усі його кути теж рівні.

Пошаговое объяснение:

Доведіть,що коли сторони многокутника,вписаного в коло, рівні, то й усі його кути теж рівні

• Многокутник називається вписаним у коло, якщо всі його вершини належать колу.

• Центром такого кола є точка перетину серединних перпендикулярів, проведених до всіх сторін многокутника.

Доведення

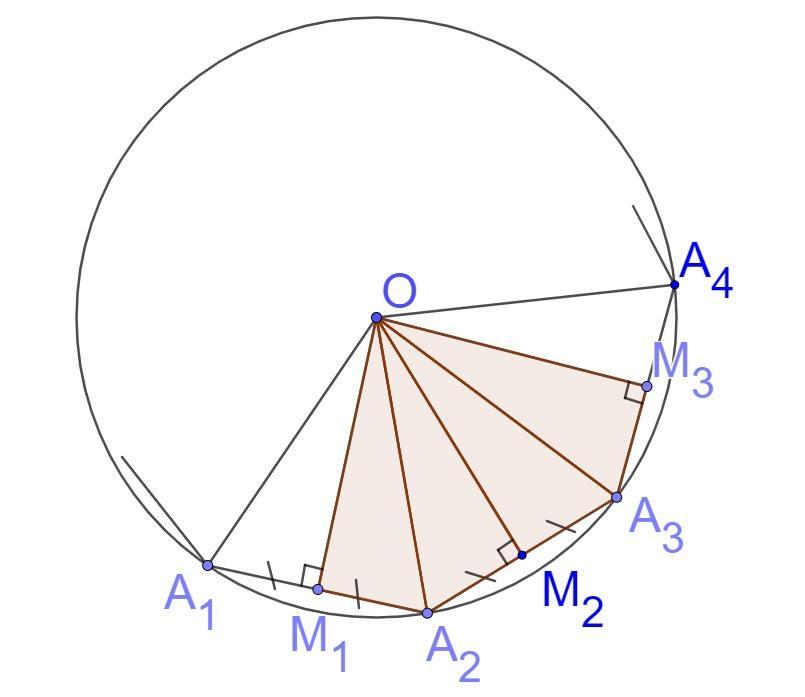
А₁А₂А₃...Аₙ - многокутник вписаний в коло з центром в точці О.

За умовою А₁А₂=А₂А₃=А₃А₄=...=Аₙ₋₁Аₙ

О - точка перетину серединних перпендикулярів. Отже:

ОМ₁⊥А₁А₂, ОМ₂⊥А₂А₃, ОМ₃⊥А₃А₄,...

А₁М₁=М₁А₂, А₂М₂=М₂А₃, А₃М₃=М₃А₄, ....

Так як сторони многокутника рівні, то:

А₁М₁=М₁А₂=А₂М₂=М₂А₃=А₃М₃=М₃А₄= ....

1. Розглянемо прямокутні трикутники ΔОМ₁А₂ і ΔОМ₂А₂ (∠ОМ₁А₂=∠ОМ₂А₂=90°)

• М₁А₂=А₂М₂

• ОА₂-спільна

ΔОМ₁А₂ = ΔОМ₂А₂ (за гіпотенузою і катетом)

Отже ∠ОА₂М₁=∠ОА₂М₂ - як відповідні кути рівніх трикутників.

2. Розглянемо прямокутні трикутники ΔОМ₂А₂ і ΔОМ₂А₃ (∠ОМ₂А₂=∠ОМ₂А₃=90°)

• А₂М₂=М₂А₃

• ОМ₂-спільна

ΔОМ₂А₂ = ΔОМ₂А₃ (за гіпотенузою і катетом)

Отже ∠ОА₂М₂=∠ОА₃М₂ - як відповідні кути рівніх трикутників.

3. Розглянемо прямокутні трикутники ΔОМ₂А₃ і ΔОМ₃А₃ (∠ОМ₂А₃=∠ОМ₃А₃=90°)

• М₂А₃=А₃М₃

• ОМ₃-спільна

ΔОМ₂А₃ = ΔОМ₃А₃ (за гіпотенузою і катетом)

Отже ∠ОА₃М₂=∠ОА₃М₃ - як відповідні кути рівніх трикутників.

4. Отримали, що: ∠ОА₂М₁=∠ОА₂М₂=∠ОА₃М₂=∠ОА₃М₃ , тобто ∠А₁А₂А₃=∠А₂А₃А₄ - кути рівні, що і треба було довести.

#SPJ1