Самостоятельная работа 4.2
Показательные уравнения и неравенства
вариант 2

Ответы на вопрос
1.
а) 0,5³ˣ⁻² = 1,
0,5³ˣ⁻² = 0,5⁰,
3х - 2 = 0,
3х = 2,
х = 2/3
б) 5 · 3ˣ = 135,
3ˣ = 27,
3ˣ = 3³,
х =3
в) 2ˣ = 32 · 4^(1/5),
2ˣ = 2⁵ · 2^(2/5),
2ˣ = 2^(5 целых 2/5),
х = 5 целых 2/5
г) 5ˣ + 5ˣ⁺² = 26,
5ˣ + 5ˣ · 5² = 26,
5ˣ(1 + 25) = 26,
5ˣ · 26 = 26,
5ˣ = 1,
5ˣ = 5⁰,
х = 0
2.
а) 5^(x² - 5x + 8) = 25,
5^(x² - 5x + 8) = 5²,
х² - 5х + 8 = 2,
х² - 5х + 6 = 0,
D = (-5)² - 4 · 1 · 6 = 25 - 24 = 1; √1 = 1
х₁ = (5 + 1)/(2 · 1) = 6/2 = 3
х₂ = (5 - 1)/(2 · 1) = 4/2 = 2
б) 6²ˣ - 7 · 6ˣ + 6 = 0,
(6ˣ)² - 7 · 6ˣ + 6 = 0,
обозначим 6ˣ = у, получим и решим уравнение
у² - 7у + 6 = 0,
D = (-7)² - 4 · 1 · 6 = 49 - 24 = 25; √25 = 5
у₁ = (7 + 5)/(2 · 1) = 12/2 = 6
у₂ = (7 - 5)/(2 · 1) = 2/2 = 1
6ˣ = 6,
6ˣ = 6¹,
х = 6;
6ˣ = 1,
6ˣ = 6°,
х = 0.
3.
а) 3ˣ< 9 · 27^(1/5),
3ˣ < 3² · (3³)^(1/5),
3ˣ < 3² · 3^(3/5),
3ˣ < 3^(2 целых 3/5), т.к. а = 3 > 1, то перейдем к неравенству
х < 2 целых 3/5,
х ∈ (-∞; 2,6)
2 целых 3/5 = 2,6
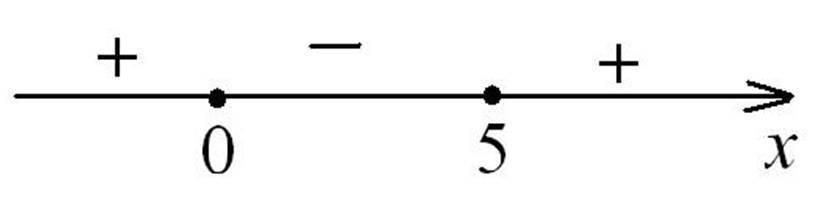
б) 0,6^(x² - 5x) ≥ 1,
0,6^(x² - 5x) ≥ 0,6°, т.к. 0 < 0,6 < 1, то прейдем к неравенству
х² - 5х ≤ 0,
х(х - 5) ≤ 0,
х ∈ [0; 5] см. рис. в приложении.