Алгебра, вопрос задал ВладимирБ , 2 месяца назад

Решите систему уравнений

Приложения:

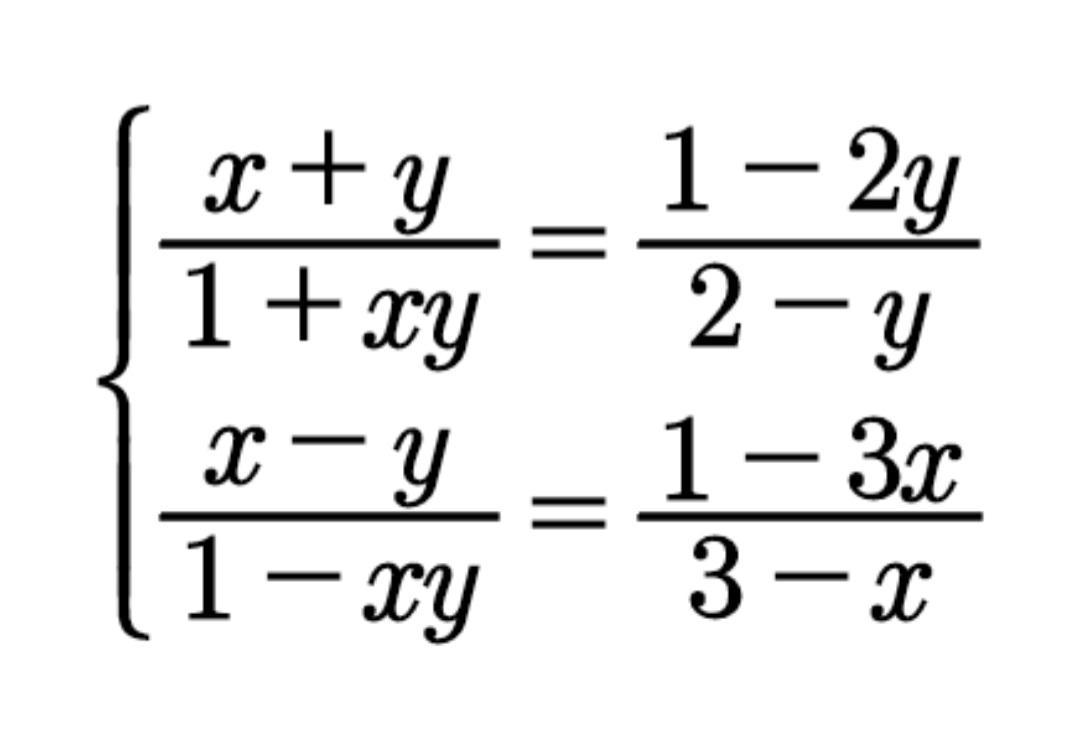
polarkat: Вернулось задание! Удалили вроде)

Ответы на вопрос

Ответил polarkat

Оказалось не таким и сложным

Решим второе уравнение для $y$ , подставив его в первое уравнение

$13x^5-55x^4+130 x^3-110 x^2+65 x-11=0$

Решим первое уравнение для $x$ , подставив его во второе уравнение

$11 y^5-35 y^4+110 y^3-70 y^2+55 y-7=0$

Они оба разрешимы, поскольку принадлежат к семейству $p_{ab}(u)=au^5+5bu^4+10au^3+10bu^2+5au+b$

В общем случае, чтобы решить $p_{ab}(u)=0$ в радикалах, сначала положим $s+t=a$ и $s-t=b$ . Это дает $s=\frac{a+b}{2}$ и $t=\frac{a-b}{2}$ . Затем

$p_{ab}(u)=(s+t)u^5+5(s-t)u^4+10(s+t)u^3+10(s-t)u^2+5(s+t)u+(s-t)=s(u+1)^5+t(u-1)^5$

$\left(\frac{1-u}{1+u}\right)^5=\frac{s}{t}\Rightarrow u=\frac{1-\sqrt[5]{s/t}}{1+\sqrt[5]{s/t}}=\frac{\sqrt[5]{t}-\sqrt[5]{s}}{\sqrt[5]{t}+\sqrt[5]{s}}$

Мы можем избавится от иррациональности в знаменатели, умножив верхнюю и нижнюю части на $\sqrt[5]{t^4}-\sqrt[5]{st^3}+\sqrt[5]{s^2t^2}-\sqrt [5]{s^3t}+\sqrt[5]{s^4}$

Следовательно

$u=\frac{t-s-2\sqrt[5]{st^4}+2\sqrt[5]{s^2t^3}-2\sqrt[5]{s^3t^2}+2\sqrt[5]{s^4t}}{s+t}=$ $=\frac{-b-\sqrt[5]{(a+b)(a-b)^4}+\sqrt[5]{(a+b)^2(a-b)^3}-\sqrt[5]{(a+b)^3(a-b)^2}+\sqrt[5]{(a+b)^4(a-b)}}{a}$