Алгебра, вопрос задал ViktorSen , 2 месяца назад

Доведіть, що для всіх а≠ ±5 значення виразу не залежить від а

Приложения:

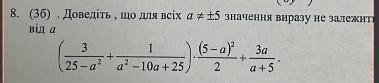
Ответы на вопрос

Ответил 7x8

Ответ:

Hе залежить від a

Объяснение:

$\displaystyle \left(\frac{3}{25-a^2}+\frac{1}{a^2-10a+25}\right)\cdot\frac{(5-a)^2}{2}+\frac{3a}{a+5}=\\\\\left(\frac{3}{(5-a)(5+a)}+\frac{1}{(5-a)^2}\right)\cdot\frac{(5-a)^2}{2}+\frac{3a}{a+5}=\\\\\left(\frac{3(5-a)}{(5-a)^2(5+a)}+\frac{5+a}{(5-a)^2(5+a)}\right)\cdot\frac{(5-a)^2}{2}+\frac{3a}{a+5}=\\\\\frac{3(5-a)+5+a}{(5-a)^2(5+a)}\cdot\frac{(5-a)^2}{2}+\frac{3a}{a+5}=\\\\\frac{15-3a+5+a}{5+a}\cdot\frac{1}{2}+\frac{3a}{a+5}=\\\\$

$\displaystyle \frac{-2a+20}{5+a}\cdot\frac{1}{2}+\frac{3a}{a+5}=\frac{2(-a+10)}{5+a}\cdot\frac{1}{2}+\frac{3a}{a+5}=\\\\\frac{-a+10}{5+a}+\frac{3a}{a+5}=\frac{-a+10+3a}{a+5}=\\\\\frac{10+2a}{a+5}=\frac{2(5+a)}{a+5}=2$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 2 месяца назад

Срочноооо помогите пожалуйста дам много балов!!

Литература, 2 месяца назад

План до твору « Бо сонце єдине»...

Химия, 2 месяца назад

В объёме 10 л (н.у.) воздуха содержится 6-10(-⁵ ) мл криптона. Рассчитайте объём (л) воздуха, в котором содержится 10¹⁶ шт Кг. Ответ с ОБЪЯСНЕНИЕМ ...

Математика, 2 месяца назад

Дана платежная матрица. Строки матрицы а - возможная прибыль предпринимателя при разных стратегиях его конкурента.Столбцы матрицы - возможные убытки конкурентов при соответствующих стратегиях...

Английский язык, 6 лет назад

5 предложений на be goin to...

Физика, 6 лет назад

определить силу с которой магнитное поле с индукцией 48гц действует на проводник длинной 50 см по которому текет ток 5 А...