Решить тригонометрическое уравнение
Приложения:
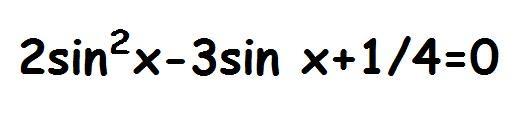
Ответы на вопрос
Ответил Misha001192
0
2sin²x - 3sinx + (1/4) = 0
Домножим обе части на 4
8sin²x - 12sinx + 1 = 0
Данное уравнение является квадратным относительно sinх, сделаем замену: sinx = a, a ∈ [-1;1], тогда
8а² - 12а + 1 = 0
D = (-12)² - 4•8•1 = 144 - 32 = 112
a₁ = (12 - 4√7)/16 = (3 - √7)/4 ≈ 0,09
sinx = (3-√7)/4
x₁ = arcsin( (3-√7)/4 ) + 2πn, n ∈ Z
x₂ = π - arcsin( (3-√7)/4 ) + 2πk, k ∈ Z
a₂ = (12 + 4√7)/16 = (3 + √7)/4 ≈ 1,41 ∉ [-1;1] ⇒ ∅
ОТВЕТ: arcsin( (3-√7)/4 ) + 2πn ; π - arcsin( (3-√7)/4 ) + 2πk , n , k ∈ Z
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Алгебра,
7 лет назад
Биология,
7 лет назад
Математика,
8 лет назад
Математика,
8 лет назад