Найти область определения функции
Приложения:
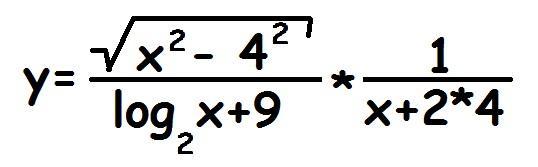
Ответы на вопрос
Ответил genius20
0
Здесь надо учесть четыре ограничения:
1) Подкоренное выражение не должно быть отрицательным:
2) Выражение под логарифмом должно быть положительным:
3) Знаменатель первой дроби должен быть ненулевым
4) Знаменатель второй дроби также должен быть ненулевым:
Теперь объединим эти промежутки (лучше сделайте это на листке бумаги, чтобы видеть наглядно): по второму условию икс положителен, поэтому первое условие сокращается до
Третье условие не удовлетворяет предыдущему, поэтому вычёркивается.
Четвёртое условие также вычёркивается как отрицательное.
Ответ:
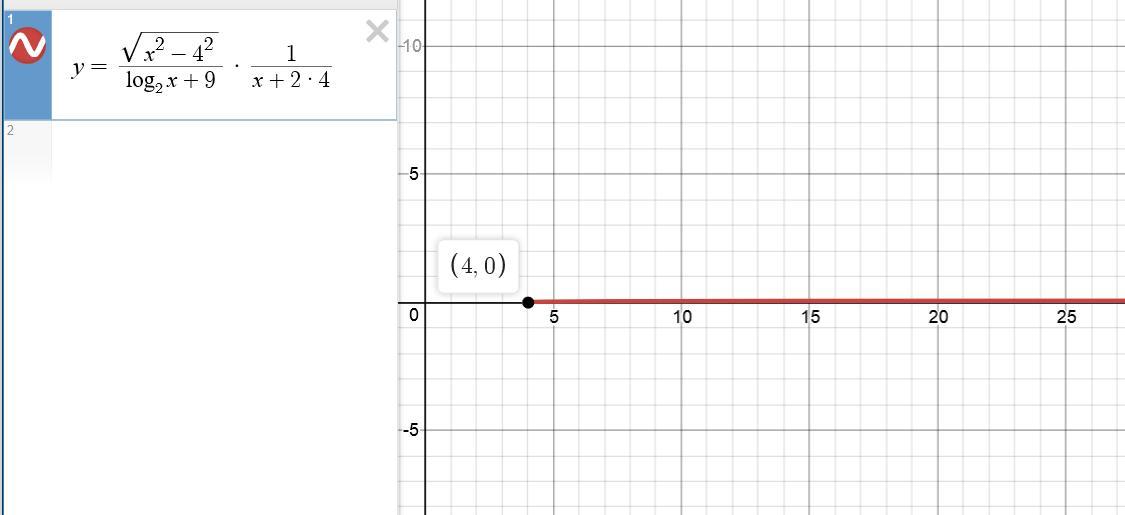
Вот так выглядит график этой функции, построенный на компьютере (см. скриншот).
P. S. Если появились какие-либо вопросы, задавайте.
Приложения:
Новые вопросы
Английский язык,
1 год назад
Русский язык,
1 год назад
Химия,
7 лет назад
История,
7 лет назад
Литература,
8 лет назад