Алгебра, вопрос задал veronica021707 , 11 месяцев назад

Рівняння - log3(x + 3) - log3(x - 1) = 1 - log3(4 - x)
Повна відповідь

Приложения:

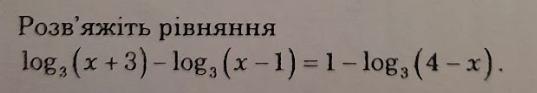
Ответы на вопрос

Ответил Universalka

1

ОДЗ :

$\displaystyle\bf\\\left\{\begin{array}{ccc}x+3 > 0\\x-1 > 0\\4-x > 0\end{array}\right \ \ \ \Rightarrow \ \ \ \left\{\begin{array}{ccc}x > -3\\x > 1\\x < 4\end{array}\right \ \ \ \Rightarrow \ \ \ x\in(1 \ ; \ 4)\\\\\\\log_{3} (x+3)-\log_{3} (x+1)=1-\log_{3} (4-x)\\\\\\\log_{3} (x+3)-\log_{3} (x+1)=\log_{3} 3-\log_{3} (4-x)\\\\\\\log_{3} \frac{x+3}{x+1} =\log_{3} \frac{3}{4-x} \\\\\\\frac{x+3}{x+1} =\frac{3}{4-x} \\\\\\(x+3)\cdot(4-x)=3\cdot(x+1)$

$\displaystyle\bf\\4x-x^{2} +12-3x=3x+3\\\\x-x^{2} +12-3x-3=0\\\\x^{2} +2x-9=0\\\\D=2^{2} -4\cdot(-9)=4+36=40=(2\sqrt{10} )^{2}\\\\\\x_{1} =\frac{-2+2\sqrt{10} }{2} =\sqrt{10} -1\\\\\\x_{2} =\frac{-2-2\sqrt{10} }{2} =-1-\sqrt{10} -ne \ podxodit\\\\\\Otvet \ ; \ \sqrt{10}-1$

kamenkovaanastasia36: Допоможіть будь ласка з останнім завданням у профілі

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 8 месяцев назад

Дано функцію ......... . Знайти .........

Алгебра, 8 месяцев назад

риведи друга и получи 15% скидку», «Приведешь двух друзей -получи 20% скидку». В таблице приведены наименование наборов, на которые действует акция. Айгуль решила воспользоваться пятничной...

Українська мова, 11 месяцев назад

Зробіть синтаксичний розбір речення, накресліть схему до нього Велике діло коли людина має чисте сумління коли ніякі тіні не каламутять не забруднюють душу (М. Стельмах). ПОЖАЛУЙСТА СРОЧНО РЕБЯТ...

Геометрия, 11 месяцев назад

срочно!!!помогите пожалуйста!!

Русский язык, 6 лет назад

Исправые ошибки в тексте. Напишите исправленный текст. ыыыы помогите пж пж пж...

Геометрия, 6 лет назад

Буду благодарен если решите...