Алгебра, вопрос задал fctdgsygfdhngfxzgsac , 8 месяцев назад

Дано функцію ......... . Знайти .........

Приложения:

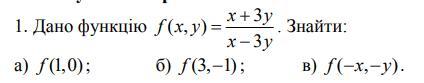
Ответы на вопрос

Ответил pushpull

Ответ:

в объяснении

Объяснение:

Чтобы найти значение функции, надо просто подставить указанные значения аргументов в формулу функции.

$\displaystyle f(x,y)=\frac{x+3y}{x-3y}; \quad x-3y\neq 0;\quad x\neq 3y\\\\\\ f(1,0) = \frac{1+3*0}{1-3*0} =1\\\\\\f(3,-1)=\frac{3+3*(-1)}{3-3*(-1)} =\frac{3-3}{3+3} =0\\\\\\$

$\displaystyle f(-x,-y)=\frac{-x+3*(-y)}{-x-3*(-y)}=\frac{-x-3y}{-x+3y} =\frac{-(x+3y)}{-(x-3y)} =f(x,y)$

fctdgsygfdhngfxzgsac: Спасибо большое)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 5 месяцев назад

Запишіть іменники у формі давального відмінка однини. 1) Відпустка,глядачка,посіпака,фізика,онука,завідувачка,слобожанка,харківка,веселка,смушка,виставка,вишивка,застібка. 2)...

Физика, 5 месяцев назад

СРОЧНО!!!!!!!! Два маленьких, одинаковых по размеру шарика, находясь на расстоянии R=0,2 м, притягиваются с силой F₁=4 мН (4*10⁻³ Н).После того, как шарики были приведены в соприкосновение и вновь...

Геометрия, 8 месяцев назад

5) В равнобедренном треугольнике АВС с основанием АС P=80 см, соотношение боковой стороны и основания равно 3:4. Найти стороны треугольника АВС. СРОЧНО ПОМОГИТЕ...

Математика, 8 месяцев назад

на уроке физкультуры ребята построили в шеренку с интервалом 1 м они набрали 20 м Сколько детей было в на уроке ...

Немецкий язык, 6 лет назад

Bilden Sie Nebensätze aus den in Klammern stehenden Wörtern und Wortgruppen. 1. Der Arzt sagte dem Kranken, dass (sich ro:ntgen lassen mu:ssen) 2. Der Junge wundert sich, dass (wieder die gleichen...

Геометрия, 6 лет назад

помогите срочно геометрия...