(QBasic) Построить равнобедренный треугольник симметричный относительно горизонтальной оси, задать его размером двух разных сторон и определить радиус описанной окружности. Вывести значения сторон и радиуса на экран монитора.
-проанализировать исходные данные
-разобрать математическое описание
-расмотреть логическую структуру решения
-написать текст программы на языке QB
-составить тестовую задачу
Ответы на вопрос
Ответил Аноним
0
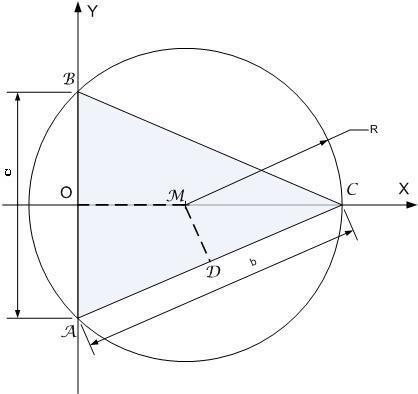
Чертёж дан во вложении.
Пусть ΔABC - равнобедренный, АВ = с - его основание, АС = ВС = b - боковые стороны. По условию треугольник симметричен относительно горизонтальной оси, так что его основание АВ должно быть перпендикулярно горизонтальной оси и при этом АО = ОВ, а вершина С попадет на горизонтальную ось. Разместим ΔABC так, чтобы основание попало на вертикальную ось.
Окружность, описанная вокруг треугольника, пройдет через все три его вершины. Точка М - центр описанной окружности, - лежит на пересечении перпендикуляров, проведенных из середин сторон треугольника. Поскольку ΔABC равнобедренный, то ОС - его высота и отрезок МС, равный радиусу окружности R, также лежит на горизонтальной оси.
Найдем высоту ОС, обозначив её через h, по теореме Пифагора.
ОС - это катет ΔAOC, AO ⊥ OC.

Площадь ΔABC находим по формуле

Для нахождения радиуса R = MC рассмотрим прямоугольные ΔAOC и ΔMDC, имеющие общий угол АСО = α

Теперь легко сделать необходимое построение.
Для этого откладываем от начала координат по горизонтальной оси отрезок ОМ и проводим из него, как из центра, окружность радиуса R. Соединяем между собой три точки пересечения окружностью осей координат и получаем треугольник с длинами сторон, равными заданным.
Ниже приводится программа на языке Microsoft QBasic, позволяющая рассчитать длину отрезка ОМ (Mx - координату х точки М) и радиус описанной окружности R по заданной длине основания с и длине боковой стороны b.
INPUT "Основание: ", c
INPUT "Боковая сторона: ", b
h = SQR(b ^ 2 - (c / 2) ^ 2)
R = b ^ 2 / (2 * h)
Mx = h - R
PRINT "Радиус равен "; R, "Координата центра равна "; Mx
Тестовое решение:
Y:qbasic>QBASIC.EXE
Основание: 6
Боковая сторона: 5
Радиус равен 3.125 Координата центра равна .875
Чтобы продолжить, нажмите любую клавишу
Пусть ΔABC - равнобедренный, АВ = с - его основание, АС = ВС = b - боковые стороны. По условию треугольник симметричен относительно горизонтальной оси, так что его основание АВ должно быть перпендикулярно горизонтальной оси и при этом АО = ОВ, а вершина С попадет на горизонтальную ось. Разместим ΔABC так, чтобы основание попало на вертикальную ось.
Окружность, описанная вокруг треугольника, пройдет через все три его вершины. Точка М - центр описанной окружности, - лежит на пересечении перпендикуляров, проведенных из середин сторон треугольника. Поскольку ΔABC равнобедренный, то ОС - его высота и отрезок МС, равный радиусу окружности R, также лежит на горизонтальной оси.
Найдем высоту ОС, обозначив её через h, по теореме Пифагора.
ОС - это катет ΔAOC, AO ⊥ OC.
Площадь ΔABC находим по формуле
Для нахождения радиуса R = MC рассмотрим прямоугольные ΔAOC и ΔMDC, имеющие общий угол АСО = α
Теперь легко сделать необходимое построение.
Для этого откладываем от начала координат по горизонтальной оси отрезок ОМ и проводим из него, как из центра, окружность радиуса R. Соединяем между собой три точки пересечения окружностью осей координат и получаем треугольник с длинами сторон, равными заданным.
Ниже приводится программа на языке Microsoft QBasic, позволяющая рассчитать длину отрезка ОМ (Mx - координату х точки М) и радиус описанной окружности R по заданной длине основания с и длине боковой стороны b.
INPUT "Основание: ", c
INPUT "Боковая сторона: ", b
h = SQR(b ^ 2 - (c / 2) ^ 2)
R = b ^ 2 / (2 * h)
Mx = h - R
PRINT "Радиус равен "; R, "Координата центра равна "; Mx
Тестовое решение:
Y:qbasic>QBASIC.EXE
Основание: 6
Боковая сторона: 5
Радиус равен 3.125 Координата центра равна .875
Чтобы продолжить, нажмите любую клавишу
Приложения:
Ответил Dadu71
0
спасибо огромное!!! я уже не знал что мне делать((( вы спасли меня!!! всего вам наилучшего !!!!!!!!!Вы очень отличный человек !!!!!!
Новые вопросы