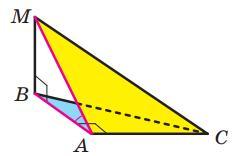
Прямокутні трикутники ABC (∠A = 90°) і ABM (∠B = 90°) мають спільний катет AB . Відрізок MB перпендикулярний до площини ABC. Відомо, що MB = 4 см, AC = 6 см, MC = 10 см. Знайдіть кут між площинами ABC і AMC.
Ответы на вопрос
Відповідь:
Пояснення:
Спочатку знайдемо довжину AB за допомогою теореми Піфагора в трикутнику ABC:
AB² = AC² + BC²
AB² = 6² + BC²
AB² = 36 + BC²
AB = √(36 + BC²)
Аналогічно, з трикутника BMC маємо:
BC² + MB² = MC²
BC² + 4² = 10²
BC² = 100 - 16
BC = √84
Підставляємо отримані значення в формулу для AB:
AB = √(36 + BC²) = √(36 + 84) = √120 = 2√30
Тепер можемо знайти синус кута між площинами ABC і AMC за допомогою векторного добутку нормалей до цих площин:
sin(∠BAM) = (n_1 x n_2) / (|n_1| |n_2|)
де n_1 і n_2 - нормалі до площин ABC і AMC відповідно.
Нормалі можна знайти, взявши векторний добуток двох векторів, що лежать у цих площинах. Наприклад, вектор AB і вектор AC лежать у площині ABC, тому їх векторний добуток дасть нормаль до площини ABC:
n_1 = AB x AC
n_1 = (2√30, 0, 0) x (0, 6, 0)
n_1 = (0, 0, 12√30)
Аналогічно, вектор MB і вектор MC лежать у площині AMC, тому їх векторний добуток дасть нормаль до площини AMC:
n_2 = MB x MC
n_2 = (0, 4, 0) x (10, 0, 0)
n_2 = (0, 0, 40)
Тепер знаходимо добуток нормалей:
n_1 x n_2 = (0, 0, 12√30) x (0, 0, 40)
n_1 x n_2 = (-480√30, 0, 0)
та їх модулі:
|n_1| = √(0² + 0² + (12√30)²) = 12√10
|n_2| = √(0² + 0² + 40²) = 40
Тоді:
sin(∠BAM) = (n_1 x n_2) / (|n_1| |n_2|)
sin(∠BAM) = (-480√30) / (12√10 * 40)
sin(∠BAM) = -√3 / 3
Отже, кут між площинами ABC і AMC можна знайти за допомогою оберненого синуса:
∠BAM = arcsin(-√3 / 3) ≈ -60°
Однак, ми отримали від'ємне значення кута, тому треба з'ясувати, чому це сталося. За звичайними умовами, кут між двома площинами повинен бути від 0° до 180°. Однак, у нашому випадку, площина AMC лежить нижче площини ABC, тому кут між ними вважається за від'ємний. Щоб отримати додатнє значення кута, треба просто взяти доповнення до 180°:
∠BAM = 180° - |-60°| = 180° + 60° = 240°
Отже, кут між площинами ABC і AMC дорівнює 240°.