Прямая АВ пересекает параллельные плоскости α, β,γ соответственно в точках А, В, С, причем АВ = 14, ВС = 4. Прямая МK пересекает эти же плоскости α, β,γ соответственно в точках М, K, Р, причем МР = 10. Найдите все значения, которые может принимать длина отрезка МK.
Ответы на вопрос
Ответил KuOV
0
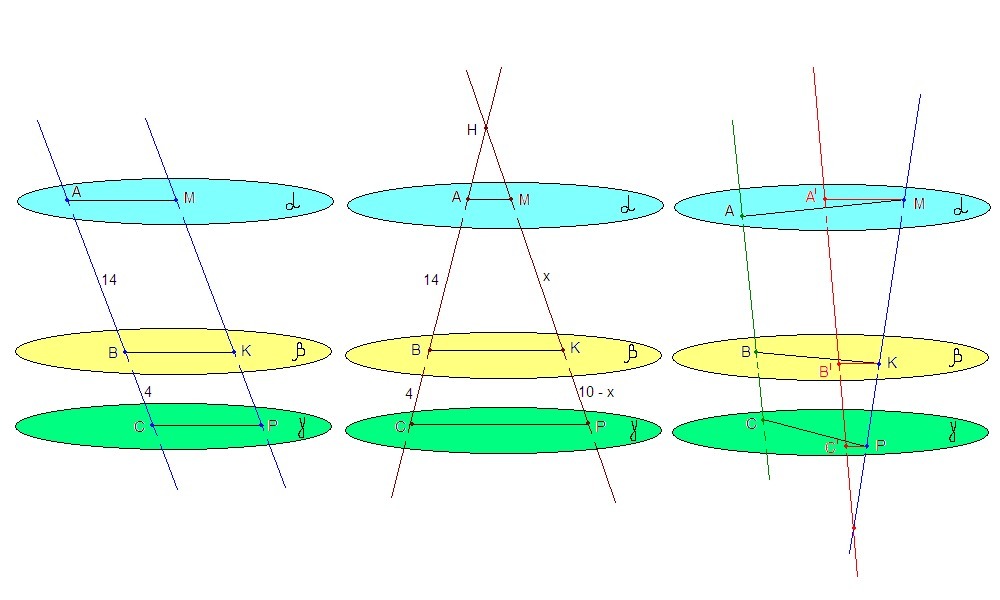
Возможны три случая взаимного расположения прямых АВ и МР:
1. АВ и МР параллельны.
Параллельные плоскости отсекают на параллельных прямых равные отрезки, значит
МК = АВ = 14
2. АВ и МР пересекаются.
Две пересекающиеся прямые АВ и МР задают плоскость, которая пересекает параллельные плоскости по параллельным прямым:
АМ║ВК║СР
Параллельные прямые отсекают на сторонах угла СНР пропорциональные отрезки:
АВ : BC = МК : КР
14 : 4 = х : (10 - х)
4х = 14·(10 - х)
4x = 140 - 14x
18x = 140
x = 70/9
МК = 70/9
3. АВ и МР скрещивающиеся.
Проведем прямую A'B', параллельную прямой АВ и пересекающуюся с прямой МР.
Параллельные плоскости отсекают на параллельных прямых равные отрезки, тогда
A'B' = AB = 14
B'C' = BC = 4
Задача сводится ко второму случаю.
1. АВ и МР параллельны.
Параллельные плоскости отсекают на параллельных прямых равные отрезки, значит
МК = АВ = 14
2. АВ и МР пересекаются.
Две пересекающиеся прямые АВ и МР задают плоскость, которая пересекает параллельные плоскости по параллельным прямым:
АМ║ВК║СР
Параллельные прямые отсекают на сторонах угла СНР пропорциональные отрезки:
АВ : BC = МК : КР
14 : 4 = х : (10 - х)
4х = 14·(10 - х)
4x = 140 - 14x
18x = 140
x = 70/9
МК = 70/9
3. АВ и МР скрещивающиеся.
Проведем прямую A'B', параллельную прямой АВ и пересекающуюся с прямой МР.
Параллельные плоскости отсекают на параллельных прямых равные отрезки, тогда
A'B' = AB = 14
B'C' = BC = 4
Задача сводится ко второму случаю.
Приложения:
Новые вопросы
Английский язык,
6 лет назад
Русский язык,
6 лет назад
Математика,
9 лет назад
Геометрия,
9 лет назад
Математика,
9 лет назад
Литература,
9 лет назад