При каких значениях параметра "а" оператор имеет тривиальное ядро, если его матрица в некотором базисе имеет вид:
Приложения:
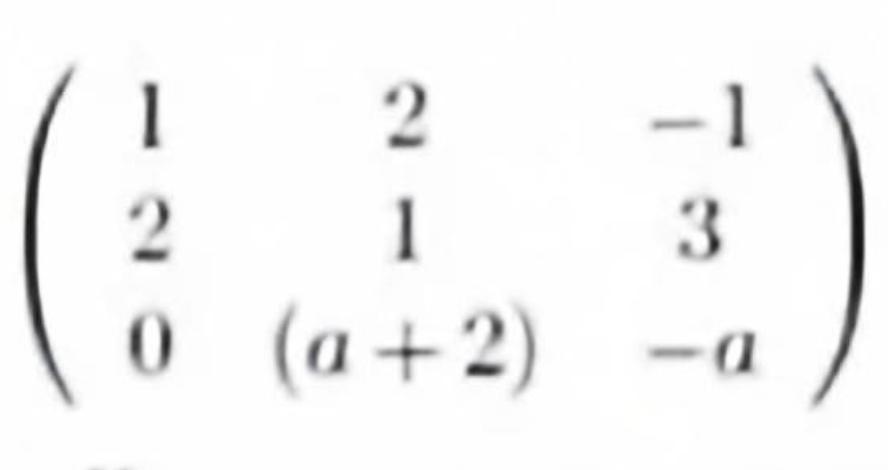
Ответы на вопрос
Ответил Guerrino
1
Подействуем оператором на некоторый вектор из пространства. Новый вектор
запишется как
, где
— матрица оператора. Тривиальность ядра равносильна тому, что решение системы
единственно (то есть только
). Это говорит о линейной независимости строк матрицы и, следовательно, о ненулевом детерминанте.
Имеем: . Поэтому при
детерминант ненулевой, а ядро тривиально.
Новые вопросы
Физика,
1 год назад
Математика,
1 год назад
Физика,
6 лет назад
Алгебра,
6 лет назад
Литература,
8 лет назад