пожалуйста Решите уравнение:↓☻
Приложения:
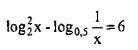
Ответы на вопрос
Ответил QuasarDreemov
0
Запишем данное уравнение в таком виде (log2(x))^2-log0,5(1/x)=6; {х>0, х не=0; <=> (log2(x))^2-log2^-1(x^-1)=6 (0,5=2^-1=1/2=0,5; 1/x=x^-1) <=> (log2(x))^2-log2(x)-6=0. Пусть log2(x)=t,
Имеем: t^2-t-6=0; D=(-1)^2+24=25; [t1=3, t2=-2. Возвращаемся к замене: а) log2(x)=3; x=2^3=8; б) log2(x)=-2; x=2^-2=1/4.
1) [(log2(8))^2-log2(8)=6] <=> [3^2-3=6] <=> [6=6];
2) [(log2(2^-2))^2-log2(2^-2>=6] <=> [(-2)^2+2=6] <=> [6=6].
Ответ: х=8, х=1/4.
Имеем: t^2-t-6=0; D=(-1)^2+24=25; [t1=3, t2=-2. Возвращаемся к замене: а) log2(x)=3; x=2^3=8; б) log2(x)=-2; x=2^-2=1/4.
1) [(log2(8))^2-log2(8)=6] <=> [3^2-3=6] <=> [6=6];
2) [(log2(2^-2))^2-log2(2^-2>=6] <=> [(-2)^2+2=6] <=> [6=6].
Ответ: х=8, х=1/4.
Новые вопросы
Русский язык,
2 года назад
Алгебра,
2 года назад
Биология,
8 лет назад
Математика,
8 лет назад
Алгебра,
9 лет назад
Математика,
9 лет назад