Математика, вопрос задал viktorcherik , 1 год назад

Помогите срочно
Дам 100 балов

Приложения:

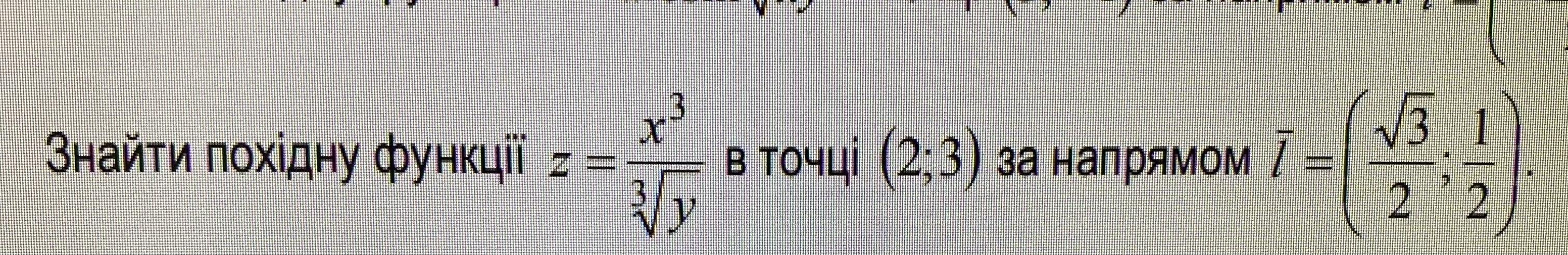
Ответы на вопрос

Ответил NNNLLL54
1

Ответ:

Найти производную функции   \bf z=\dfrac{x^3}{\sqrt[3]{\bf y}}   в точке  М₀(2;3)  по направлению

\overline{l}=\Big(\dfrac{\sqrt3}{2}\ ;\ \dfrac{1}{2}\Big)  .

|\, \overline{l}\, |=\sqrt{\dfrac{3}{4}+\dfrac{1}{4}}=1\ \ ,\ \ cos\alpha =\dfrac{\sqrt3}{2}\ \ ,\ \ cos\beta =\dfrac{1}{2}  

Вычислим частные производные в точке   М₀(2;3)  .

z'_{x}=\dfrac{3x^2}{\sqrt[3]{y}}\ \ ,\ \ \ z'_{x}(M_0)=\dfrac{3\cdot 2^2}{\sqrt[3]{3}}=4\sqrt[3]{9}\\\\\\z'_{y}=x^3\cdot \Big(-\dfrac{1}{3}\, y^{-\frac{4}{3}}\Big)=-\dfrac{x^3}{3\sqrt[3]{y^4}}\ \ ,\ \ z'_{y}(M_0)=-\dfrac{8}{3\sqrt[3]{3^4}}=-\dfrac{8}{9\sqrt[3]{3}}  

Запишем производную по направлению в точке  М₀ :

\dfrac{\partial z}{\partial \overline{l}}=z'_{x}(M_0)\cdot cos\alpha +z'_{y}(M_0)\cdot cos\beta \\\\\dfrac{\partial z}{\partial \overline{l}}=4\sqrt[3]{9}\cdot \dfrac{\sqrt3}{2}-\dfrac{8}{9\sqrt[3]{3}}\cdot \dfrac{1}{2}=\dfrac{36\sqrt[3]{27}\cdot \sqrt3-8}{18\sqrt[3]{3}}=\dfrac{108\cdot \sqrt3-8}{18\sqrt[3]{3}}=6\sqrt[6]{3}-\dfrac{4\sqrt[3]{9}}{27}  

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Математика, 11 месяцев назад
Від рулону тканини кравчиня відрізала на костюм 5 м, на пальто 3м,а на сукню-2м. Скільки всього метрів тканини відрізала кравчиня?
Математика, 11 месяцев назад
допоможіть будь ласка ​...
Математика, 1 год назад
В лифт 8-этажного дома вошли 5 человек. Каждый независимо друг от друга может выйти на любом этаже, начиная со второго. Какова вероятность того, что все вышли на разных этажах ? решение пожалуйста...
Алгебра, 1 год назад
даю 60 балов!! срочно​...
Английский язык, 6 лет назад
How many syllables? We held on to the kite string. Быстрее!!!!!!!
Русский язык, 6 лет назад
Помогите пожалуйста ( вставить пропущенные буквы ) !!!