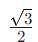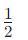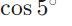Помогите с заданиями.

Ответ:

Решение:

sin~78^{\circ}cos~18^{\circ}-sin~18^{\circ}cos~78^{\circ} = sin(78^{\circ}-18^{\circ}) = sin~60^{\circ} = \frac{\sqrt{3}}}{2}

cos~66^{\circ}cos~6^{\circ}+sin~66^{\circ}sin~6^{\circ} = cos(66^{\circ}-6^{\circ}) = cos~60^{\circ} = \frac{1}{2}

cos~20^{\circ}cos~25^{\circ}-sin~20^{\circ}sin~25^{\circ} = cos(20^{\circ}-25^{\circ}) = cos~-5^{\circ} = \cos5^{\circ}

\frac{tg10^{\circ}+tg35^{\circ}}{1-tg10^{\circ}tg35^{\circ}} = \frac{\frac{\sin10^{\circ}}{\cos10^{\circ}}+\frac{\sin35^{\circ}}{\cos35^{\circ}}}{1- \frac{\sin10^{\circ}}{\cos10^{\circ}}\cdot\frac{\sin35^{\circ}}{\cos35^{\circ}}} = \frac{\sin10^{\circ}\cos35^{\circ}+\cos10^{\circ}\sin35^{\circ}}{\cos10^{\circ}\cos35^{\circ}-\sin10^{\circ}\sin35^{\circ}} = \frac{\sin(10^{\circ}+35^{\circ})}{\cos(10^{\circ}-35^{\circ})} = \frac{\sin45^{\circ}}{\cos(-25^{\circ})} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}} = \boxed{1}

Ответ:

1.

2.

3.

4. 1

Пошаговое объяснение: