Помогите с геометрией пожалуйста 100 баллов
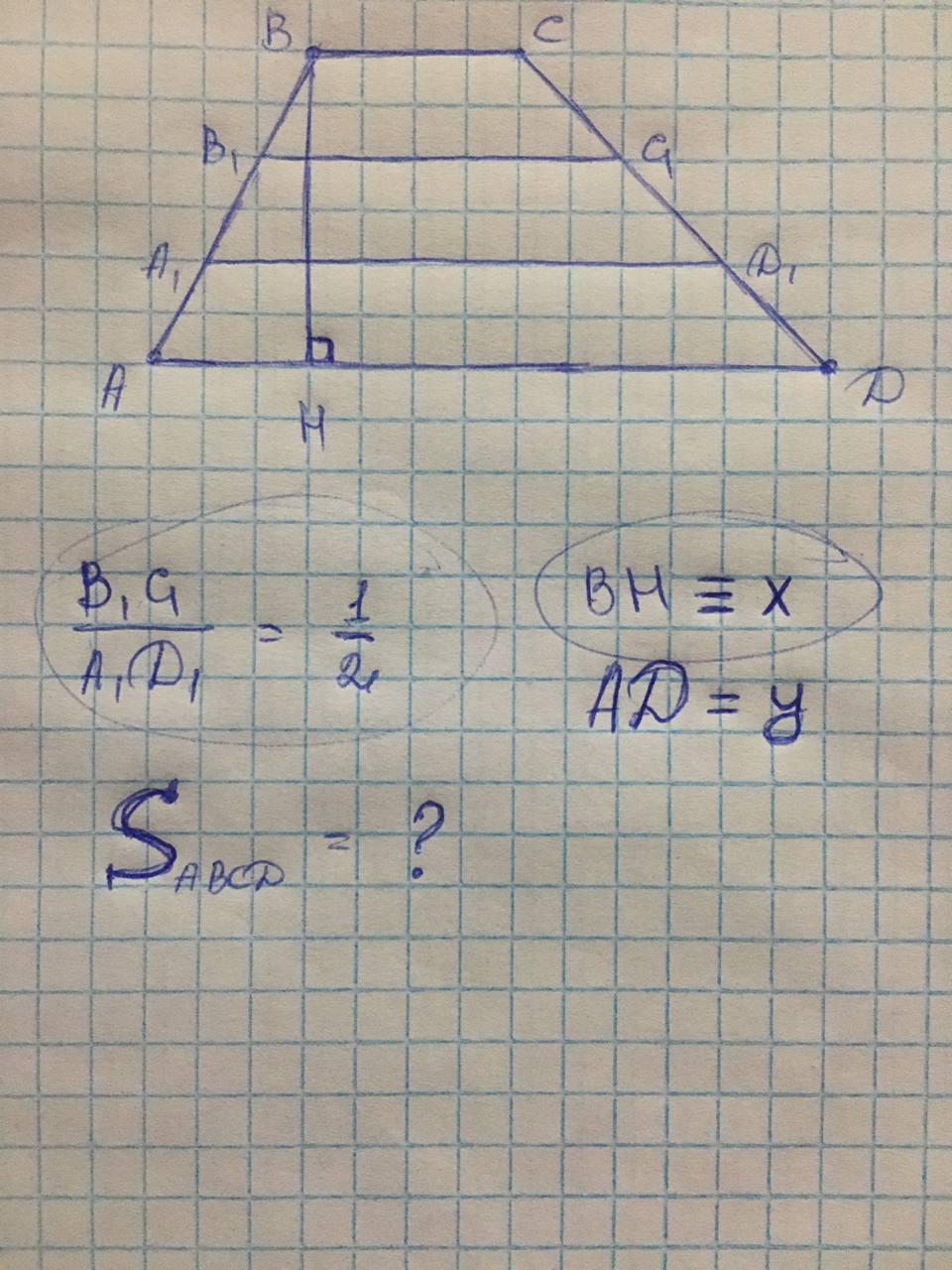
Ответы на вопрос
Відповідь:
S = 1/2 × Х × У
Пояснення:
Трапеция АВСD разбита на три части параллельными прямыми ( АD || А1D1 || В1С1 || ВС ). Отрезки АА1 = А1В1 = В1В. Высота трапеции ВН = Х, а основание АD = У. Отношение отрезков В1С1 / А1D1 = 1 / 2. Необходимо найти площадь трапеции.
Рассмотрим трапецию АВ1С1D. Отрезок А1D1 - является её средней линией.
А1D1 = ( АD + В1С1 ) / 2 = АD / 2 + В1С1 / 2
Из условия задачи извесно, что:
В1С1 / А1D1 = 1 / 2
Отсюда:
А1D1 = 2 × В1С1
Подставим это выражение в уравнение для средней линии:
2 × В1С1 = АD / 2 + В1С1 / 2
Умножим обе стороны уравнения на два, получаем:
4 × В1С1 = АD + В1С1
4 × В1С1 - В1С1 = АD
АD = 3 × В1С1
Так как АD = У, то:
3 × В1С1 = У
В1С1 = У / 3
Из уравнения для средней линии получаем:
А1D1 = ( У + У / 3 ) / 2
А1D1 = 4/3 × У / 2 = 4/6 × У = 2/3 × У
Рассмотрим трапецию А1ВСD1. Отрезок В1С1 - является её средней линией.
В1С1 = ( А1D1 + ВС ) / 2 = А1D1 / 2 + ВС / 2
Выше мы нашли, что:
В1С1 = У / 3
А1D1 = 2/3 × У
Подставим эти выражения в уравнение для средней линии:
У / 3 = 2/3 × У / 2 + ВС / 2
Умножим обе стороны уравнения на два, получаем:
2/3 × У = 2/3 × У + ВС
ВС = 2/3 × У - 2/3 × У = 0
ВЫВОД: ПРИ СОБЛЮДЕНИИ УСЛОВИЯ ЗАДАЧИ, ЧТО ОТРЕЗКИ В1С1 И А1D1 ОТНОСЯТСЯ ДРУГ К ДРУГУ КАК 1 / 2 ТРАПЕЦИЯ АВСD ВЫРОЖДАЕТСЯ В ТРЕУГОЛЬНИК АВD С ВЫСОТОЙ ВН = Х , И ОСНОВАНИЕМ АD = У. ЗАДАЧА СВОДИТСЯ К НАХОЖДЕНИЮ ПЛОЩАДИ ТРЕУГОЛЬНИКА ПО ИЗВЕСНОМУ ОСНОВАНИЮ И ПРОВЕДЕННОЙ К ЭТОМУ ОСНОВАНИЮ ВЫСОТЕ.
S = 1/2 × ВН × АD = 1/2 × Х × У