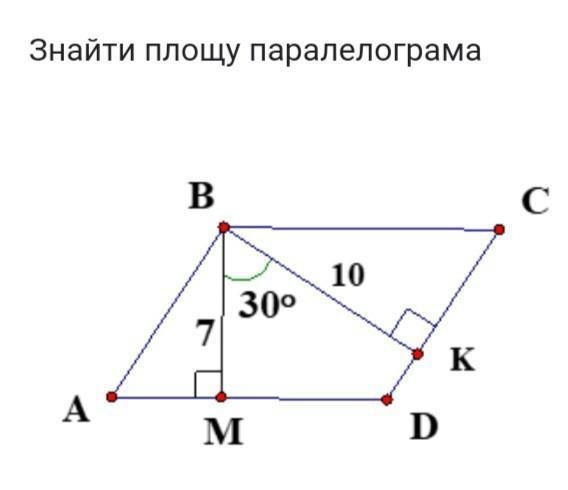
помогите пожалуйста, очень срочно, знайти площу параллелограмма ​

Решение.

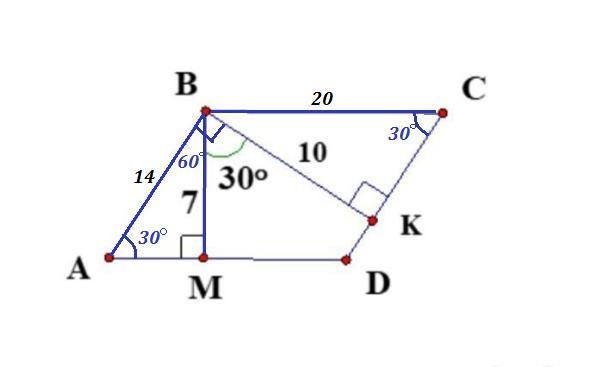
АВСД - параллелограмм , угол между высотами ВМ и ВК равен 30° ,

ВМ=7 ,  ВК=10 .

Так как высота  ВК ⊥ СД , то ВК ⊥ АВ в силу параллельности АВ и СД . Значит , ∠АВК=90° .

Тогда ∠АВМ=∠АВК-∠МВК = 90°-30°=60° .

ΔАВМ - прямоугольный ,∠ВАМ=90°-∠АВМ=90°-60°=30° .

Катет ВМ лежит против угла в 30° , значит он равен половине гипотенузы АВ . Тогда АВ=2 * 7 = 14 .

Площадь параллелограмма АВСД равна произведению стороны, умноженной на высоту, проведённую к этой стороне, то есть

S = АВ * ВК = 14 * 10 = 140 .

Ответ:  S=140 .

  Замечание .  Исходя из решения можно сделать вывод, что угол между высотами параллелограмма , проведёнными из вершины тупого угла, равен острому углу параллелограмма .

В этой задаче  ∠ВСК=∠ВАМ=30°  и  катет  ВК=10  в  ΔВСК  ⇒  ВС=20 .