помогите пожалуйста!!!!​
Даю 20 баллов!!!!!!

Ответ:

Диагональ равнобокой трапеции ABCD равна 10 ед.

Пошаговое объяснение:

Требуется найти диагональ равнобокой трапеции ABCD.

Дано: ABCD - равнобокая трапеция;

S (ABCD) = 48

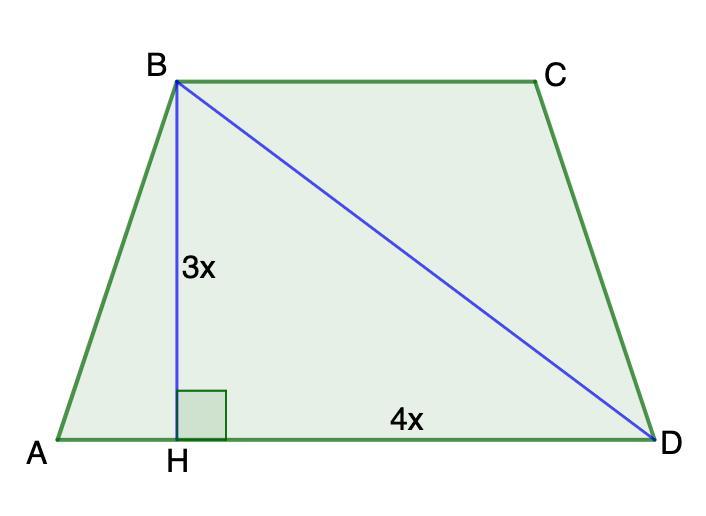
BH - высота;

ВН : НD = 3 : 4.

Найти: BD.

Решение:

1. ВН : НD = 3 : 4 (условие)

Пусть х - коэффициент пропорциональности.

Тогда ВН = 3х, а НD = 4х.

2. Рассмотрим ABCD - равнобокую трапецию.

• Высота, опущенная из вершины тупого угла на большее основание, делит его на части, большая из которых равна полусумме оснований.

⇒

• Площадь трапеции равна произведеню полусуммы оснований на высоту.

⇒

BH = 3х = 2 · 3 = 6;

HD = 4x = 2 · 4 = 8.

3. Рассмотрим ΔHBD - прямоугольный.

По тереме Пифагора:

BD² = BH² + HD² = 36 + 64 = 100

BD = √100 = 10

Диагональ равнобокой трапеции ABCD равна 10 ед.