помогите пожалуйста!!!
Приложения:
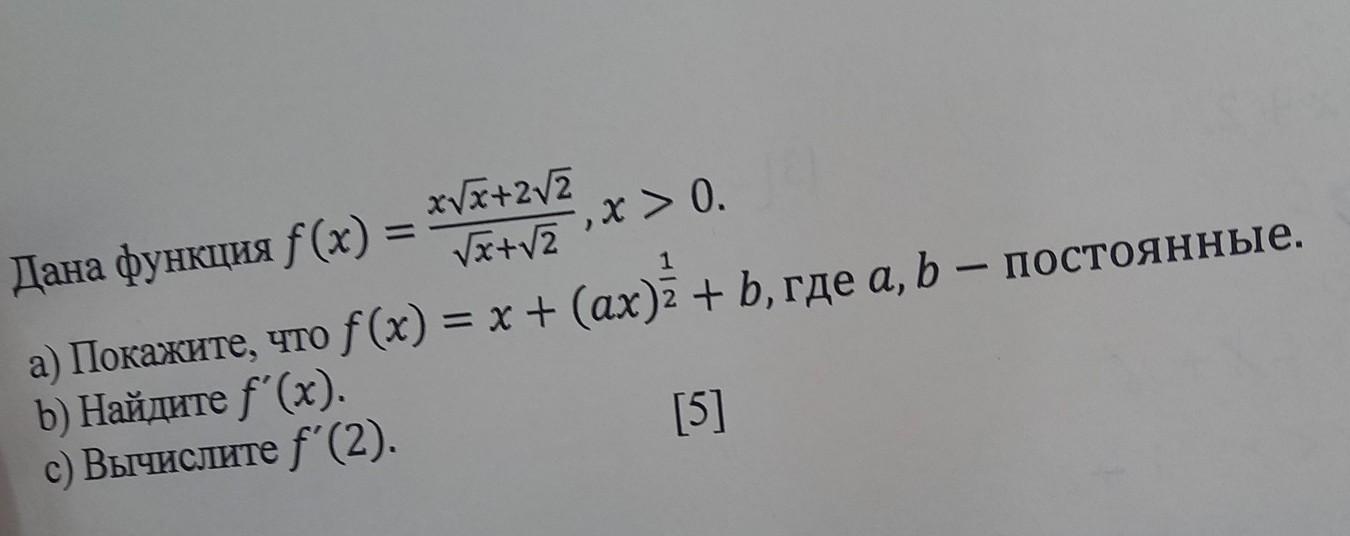
Ответы на вопрос
Ответил ilababaev97
1
Ответ:
а) Раскроем скобки под корнем:
√x+2√2 √x+√2x = √(x^2 + 2√2x^3 + 4x)
Заметим, что x^2 + 2√2x^3 + 4x = (x√2 + √2x)^2 + x^2. Поэтому:
√(x^2 + 2√2x^3 + 4x) = √((x√2 + √2x)^2 + x^2) = x√2 + √2x + о(1)
Таким образом,
f(x) = x(x√2 + √2x + о(1)) = x^2√2 + 2x^2 + о(x^2) = x^2(√2 + о(1)) + x^2 + о(x^2) = x^2(1 + √2) + ax + b
где a = 0 (так как нет слагаемых первой степени), b = 0 (так как f(0) = 0), и мы использовали обозначение о(x^n), чтобы указать на более высокие порядки малости.
Таким образом, f(x) = x^2(1 + √2).
b) Найдем производную:
f'(x) = 2x(1+√2).
с) Чтобы вычислить интеграл, нам нужно знать пределы интегрирования. Если они не указаны, то мы не можем вычислить интеграл.
Объяснение:
Новые вопросы
Математика,
8 месяцев назад
Геометрия,
8 месяцев назад
Геометрия,
11 месяцев назад
Информатика,
6 лет назад
Биология,
6 лет назад