Перимитр описаної прямокутною трапеції дорівнює 72см, а більша бічна сторона 19см. Знайди радіус кола, вписаного в трапецію?

Ответ:

8,5 см.

Объяснение:

Периметр описанной прямоугольной трапеции равен 72 см, а большая боковая сторона 19 см. Найти радиус окружности, вписанной в трапецию.

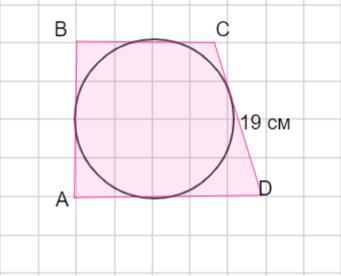
Пусть дана прямоугольная трапеция АВСD. Окружность вписана в данную трапецию.

Если окружность вписана в четырехугольник, то суммы противолежащих сторон равны.

Тогда АВ + СD = ВС +АD.

Если периметр трапеции Р = 72 см, то АВ + СD = ВС +АD= 72 : 2 = 36 см.

Если большая  боковая сторона СD равна 19 см, то

АВ = 36 -19 = 17 см.

Меньшая боковая сторона прямоугольной трапеции равна диаметру вписанной окружности. Тогда радиус в два раза меньше.

17 : 2 = 8,5 см - радиус окружности, вписанной в трапецию.

#SPJ1