Не могу сделать третий номер. Помогите, пожалуйста. Тема: правильные многогранники.

Ответы на вопрос
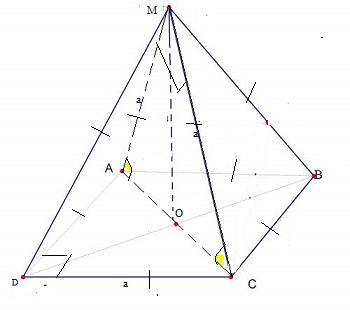
Объяснение: см. во вложении, ответ 45 градусов.

В правильной 4-х угольной пирамиде найти угол наклона бокового ребра к плоскости основания , если все ребра равны а.
Объяснение:
Углом между боковым ребром и плоскостью (АВС) является угол между наклонной и проекцией этой наклонной на плоскость ⇒например ∠МСА.
Т.к. пирамида правильная , то высота проецируется в центр основания-точку пересечения диагоналей квадрата.
Вариант решения 1
Диагональ квадрата , по т. Пифагора √(а²+а²)=а√2.
ΔАСМ-равнобедренный , АС=а√2, АМ=а, СМ=а.
По т. обратной т. Пифагора (Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник прямоугольный)
АМ²+СМ²=а²+а²=2а²
АС²=(а√2)²=2а². Т.к. АМ²+СМ²=АС²⇒ ΔАСМ прямоугольный равнобедренный ∠МАС=∠МСА=90°:2=45°
Вариант решения 2.( спасибо oganesbagoyan)
ΔABC-прямоугольный равнобедренный с углами 90°,45°,45° по свойству диагоналей квадрата.
ΔABC = ∆AMC по трем сторонам :АС-общая, АМ=СМ=АВ=ВС=а ⇒ соответственные элементы равны⇒∠МСА=45°.