Найти производные заданных функций
Приложения:
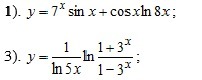
Ответы на вопрос
Ответил Аноним
0
1) y' = (7^xSinx + Cosxln8x)' =
= 7^x*ln7Sinx + 7^xCosx - Sinxln8x + Cosx*(1/8х)* 8=
=7^x*ln7Sinx + 7^xCosx - Sinxln8x + Cosx*(1/х)
3) y'=((ln5x)^-1 *ln((1 +3^x)/(1 -3^x)) )'=
= -(ln5x)^-2*5* ln((1 +3^x)/(1 -3^x)) +
+ (ln5x)^-1* (1-3^x)/(1 +3^x) *((1 +3^x)/(1 -3^x))' =
=-5/ln²5x *ln((1 +3^x)/(1 -3^x)) +
+ 1/ln5x*(1-3^x)/(1 +3^x) * (3^x*ln3(1-3^x)+(1 +3^x)*3^xln3)/(1 - 3^x)²
= 7^x*ln7Sinx + 7^xCosx - Sinxln8x + Cosx*(1/8х)* 8=
=7^x*ln7Sinx + 7^xCosx - Sinxln8x + Cosx*(1/х)
3) y'=((ln5x)^-1 *ln((1 +3^x)/(1 -3^x)) )'=
= -(ln5x)^-2*5* ln((1 +3^x)/(1 -3^x)) +
+ (ln5x)^-1* (1-3^x)/(1 +3^x) *((1 +3^x)/(1 -3^x))' =
=-5/ln²5x *ln((1 +3^x)/(1 -3^x)) +
+ 1/ln5x*(1-3^x)/(1 +3^x) * (3^x*ln3(1-3^x)+(1 +3^x)*3^xln3)/(1 - 3^x)²
Ответил tryumashev
0
спасибо, скажите пожалуйста в третьем примере во втором выражении последняя запятая относится ко всему выражению или только к последней скобке?
Ответил Аноним
0
знак производной относится ко всей функции...
Ответил tryumashev
0
ясно, спасибо!
Ответил Аноним
0
))
Новые вопросы