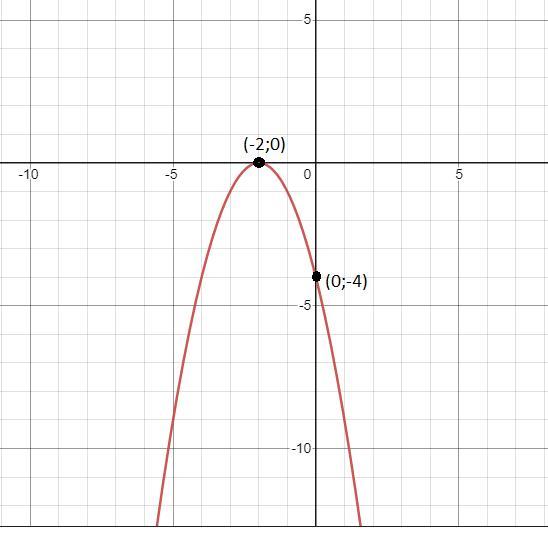
Найдите координаты вершины параболы и постройте график функции y = -x²-4x-4. По графику опридилите точки ,которые лежат на оси Ох.

Ответ:

Вершина параболы будет иметь координаты (- 2; 0).

График в прикрепленном файле.

Точка которая лежит на оси Ох - это вершина параболы, ее координаты (- 2; 0).

Пошаговое объяснение:

Требуется найти координаты вершины параболы и построить график функции у = - х² - 4х - 4, определить по графику точки которые лежат на оси Ох.

1) Найдем координаты вершины параболы у = - х² - 4х - 4.

Сначала найдем координату х₀, по формуле .

Подставим полученное значение х₀ в данную функцию и вычислим значение у₀:

у = - (- 2)² - 4 * (- 2) - 4 = - 4 + 8 - 4 = 0

Значит вершина параболы будет иметь координаты (- 2; 0).

2) Поскольку коэффициент при х² отрицательный, ветки параболы будут направлены вниз.

3) Найдем точку пересечения графика функции с осью Оу.

У точки пересечения графика с осью Оу координата х = 0. Подставим в выражение функции и получим координату у.

у = - 0² - 4 * 0 - 4 = -4

Точка пересечения графика функции с осью Оу имеет координаты (0 ; -4).

4) Построим график функции по полученным точкам (прикрепленный файл)

5) Точка которая лежит на оси Ох - это вершина параболы, ее координаты (- 2; 0).