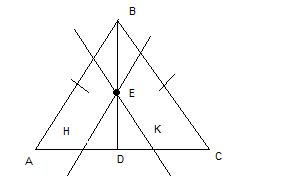
На биссектрисе BD равнобедренного треугольника ABC взята точка Е . Через эту точку проведены прямые, параллельные сторонам AB и ВС и пересекающие основание АС в точках Н и К. Докажите, что АН=КС
Ответы на вопрос
Ответил Safecracker
0
1. Поскольку АСВ - равнобедренный, то BD является также и медианой, и AD=DC
2. Треугольники АВС и НЕК подобны по первому признаку подобия: два угла одного треугольника соотетственно равны двум углам другого. В нашем случае <A=<EHK как соответственные углы при пересечении двух параллельных прямых АВ и НЕ секущей АС, а <C=<EKH тоже как соответственные углы при пересечении двух параллельных прямых ВС и ЕК секущей АС. Значит треугольник НЕК также равнобедренный, и HD=DK.
3. AD=AH+HD, DC=DK+KC, но AD=DC, поэтому можно записать:
АН+HD=DK+KC, отсюда
AH=DK+KC-HD, но HD=DK, можно записать так:
AH=DK+KC-DK, получаем
АН=КС
2. Треугольники АВС и НЕК подобны по первому признаку подобия: два угла одного треугольника соотетственно равны двум углам другого. В нашем случае <A=<EHK как соответственные углы при пересечении двух параллельных прямых АВ и НЕ секущей АС, а <C=<EKH тоже как соответственные углы при пересечении двух параллельных прямых ВС и ЕК секущей АС. Значит треугольник НЕК также равнобедренный, и HD=DK.
3. AD=AH+HD, DC=DK+KC, но AD=DC, поэтому можно записать:
АН+HD=DK+KC, отсюда
AH=DK+KC-HD, но HD=DK, можно записать так:
AH=DK+KC-DK, получаем
АН=КС
Приложения:
Ответил OxxyKisa
0
спасибо, огромное :)
Новые вопросы