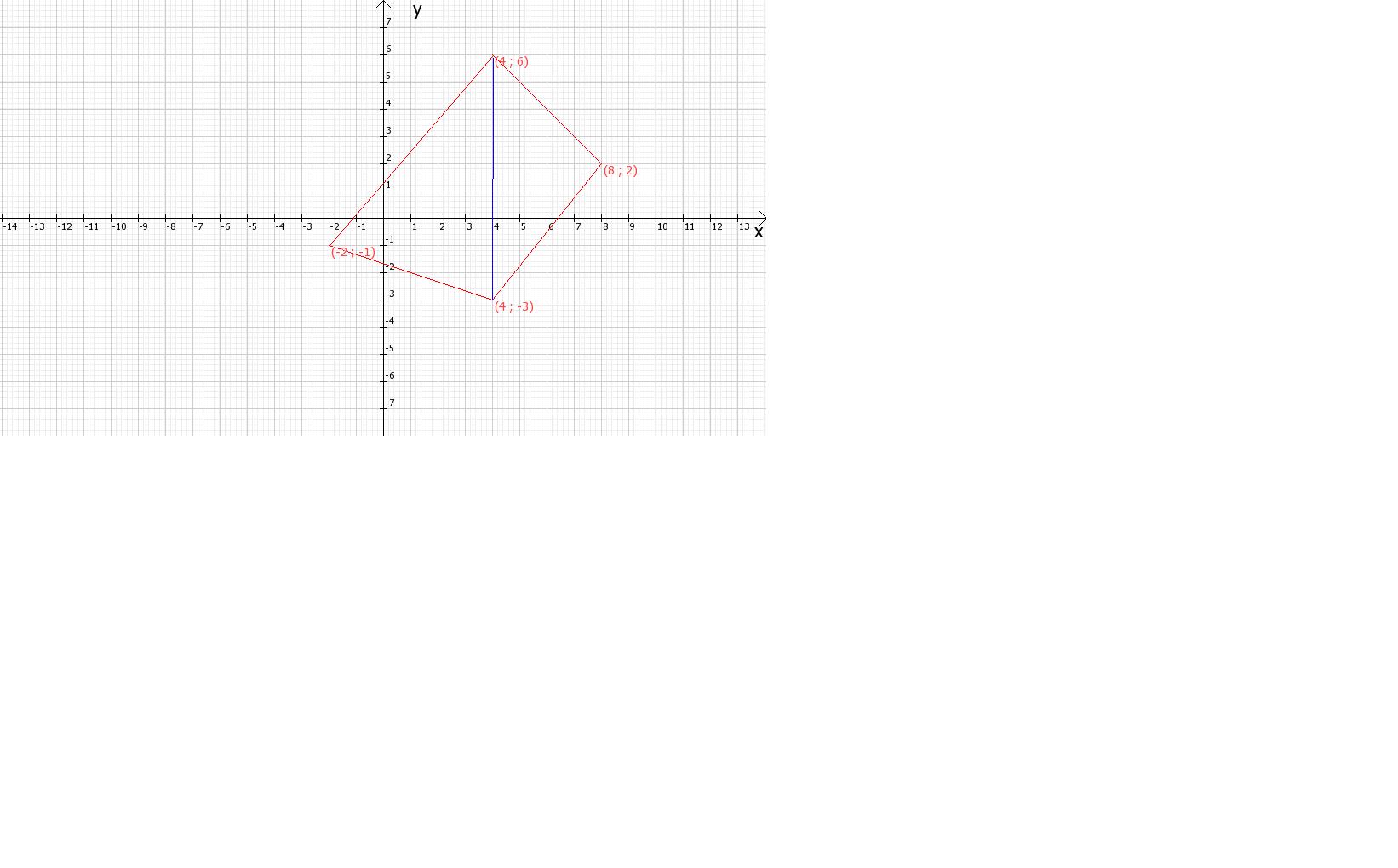
Найдите площадь четырехугольника ABCD с вершинами в точках A (4; 6), B (8; 2), C (4; -3), D (-2; -1)
Ответы на вопрос
Ответил Матов
0
найлем для начало стороны
AB=√(8-4)^2+(2-6)^2 =√ 16 +16=2√8
CD=√(-2-4)^2+(-1+3)^2 =√36+4 =√40
BC=√(4-8)^2+(-3-2)^2=√16+25=√41
AD=√(-2-4)^2+(-1-6)^2=√36+49=√85
на рисунке можно видеть что это трапеция выходит, можно раздлить эту трапецию на два треугольника затем найти площадь каждой и суммировать
Площадь треугольника S=ab/2*sina
найдем угол между АВ и AD через скаляр
AB {4;-4}
AD{-6;-7}
cosa=4*-6+ 4*7 / √32*85 = 4/√2720
теперь sina=√1-16/2720=52/√2720
теперь площадь S= 52/√2720 * √2720/2 = 26
теперь площадь другого треугольника
опять угол
B (8; 2), C (4; -3), D (-2; -1)
ВС={-4;-5}
CD={-6;2}
cosa= 24-10/√1640 = 14/√1640
sina = √(1-(14^2/1640))= 38/√1640
S=√(41*40)/2 * (38/√1640) = 19
S=26+19=45 площадь искомая
Приложения:
Новые вопросы