как решить уравнение (2x+3)^2+7(2x+3)=8
и неравенство x^2+9x+20/x+4>0
Ответы на вопрос
Ответил sintiyaberk
0
Для того, чтоб найти значения х, при которых числитель обращается в 0, воспользуемся формулой Кардано.
Находим значения:
Теперь применяем саму формулу Кардано:
Находим х.
Есть еще два корня, но они будут комплексными.
Возвращаясь к неравенству получим:
x∈(-∞; -8,8)∨(0; +∞) См. рис.
Приложения:
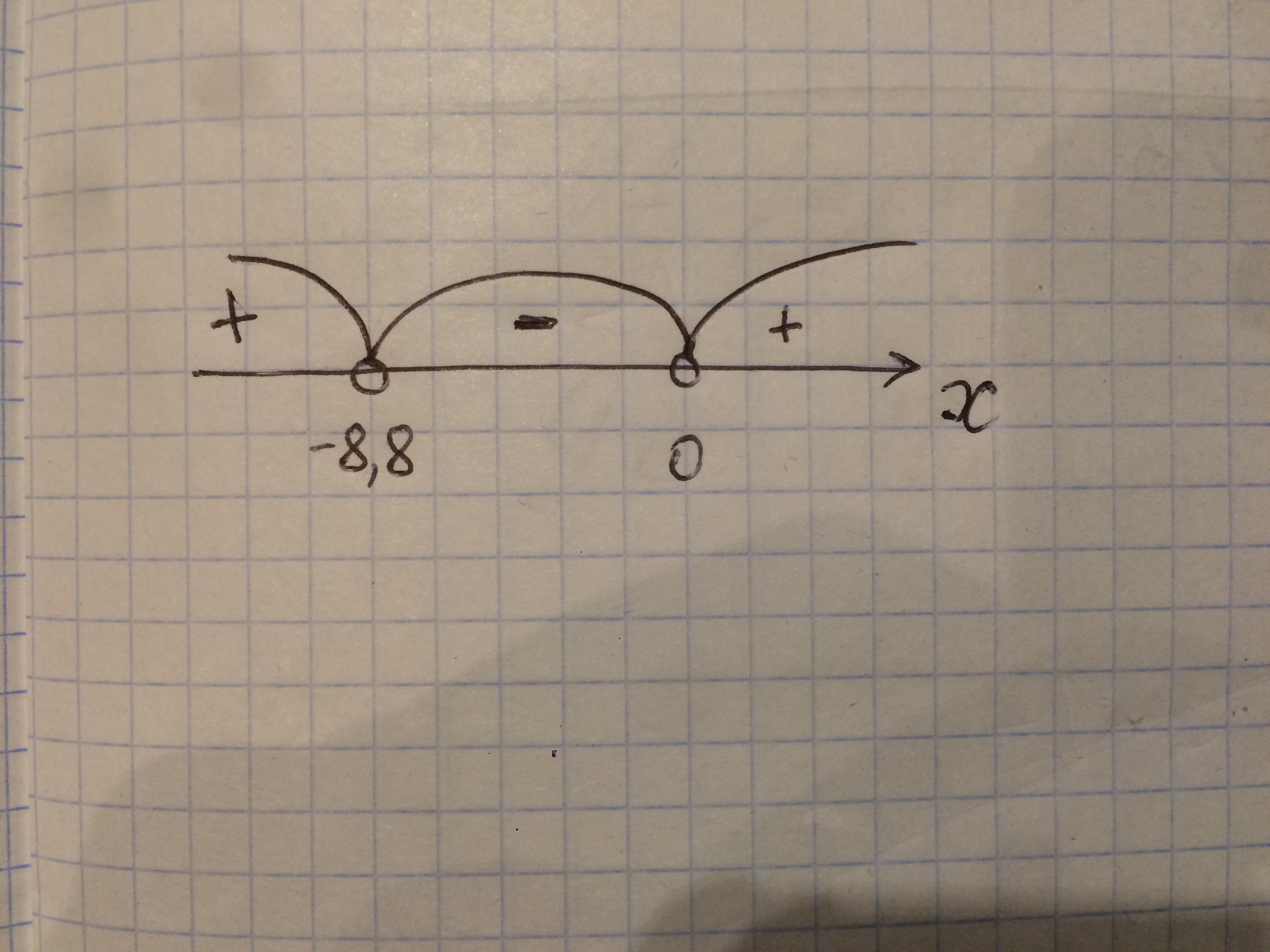
Новые вопросы