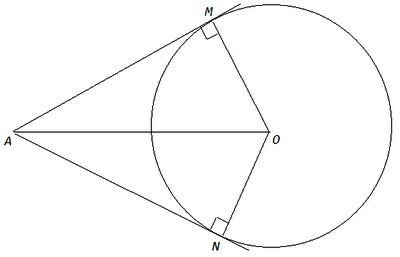
из точки a к окружности с центром o проведены две касательные am и an m и n точки касания рис 37 известно что угол mon=100 градусов найдите угол mao
Ответы на вопрос
Ответил siestarjoki
0
Радиус, проведенный в точку касания, перпендикулярен касательной, ∠AMO=∠ANO=90. В четырехугольнике AMON сумма противоположных углов равна 180, следовательно сумма другой пары противоположных углов так же равна 180, ∠MAN+∠MON=180 <=> ∠MAN=180-100=80. Касательные из одной точки составляют равные углы с прямой, проходящей через эту точку и центр окружности, AO - биссектриса ∠MAN, ∠MAO=80/2=40.
ИЛИ
Отрезки касательных, проведенных из одной точки, равны, AM=AN. Радиус, проведенный в точку касания, перпендикулярен касательной, ∠AMO=∠ANO=90. OM=ON, радиусы. △AMO=△ANO по двум катетам, ∠MOA=∠NOA=∠MON/2=50. Сумма острых углов прямоугольного треугольника равна 90, ∠MAO=90-∠MOA=40.
Приложения:
Новые вопросы
Математика,
7 лет назад
География,
8 лет назад