Алгебра, вопрос задал fctdgsygfdhngfxzgsac , 11 месяцев назад

Дослідити інтеграл на збіжність.

Приложения:

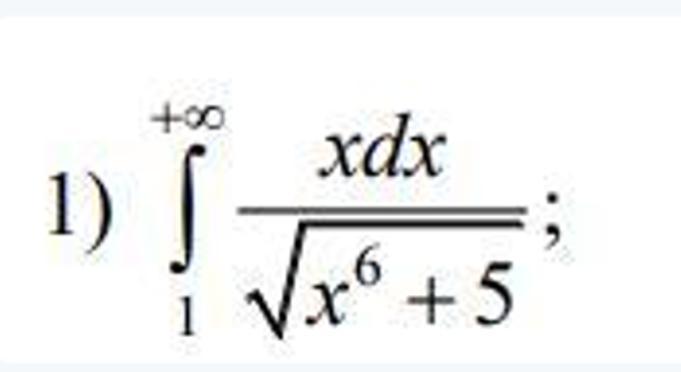
Ответы на вопрос

Ответил reygen

Ответ: Сходится

Объяснение:

Первый признак сравнения :

Если на промежутке [ a ; +∞ ) непрерывные функции f(x) и φ(x) удовлетворяют условию 0 ≤ f(x) ≤ φ(x), то если

$1) \int\limits^{+\infty }_a {\varphi(x) } \, dx$ сходится, то и $\int\limits^{+\infty }_a {f(x) } \, dx$ сходится

$2) \int\limits^{+\infty }_a {f(x) } \, dx$ расходится, то и расходится $\int\limits^{+\infty }_a {\varphi(x) } \, dx$

Шаблонный интеграл первого рода:

$\int\limits^{+\infty }_a {\frac{1}{x^p} } \, dx$

Сходится при p > 1, и расходится при p ≤ 1

Переходим к решению

$\displaystyle \int\limits^{+\infty}_1 {\frac{x dx}{\sqrt{x^6 + 5} } } \, dx$

1)При x ≥ 1

$\frac{x }{\sqrt{x^6 + 5} } > 0$

2)Также при x ≥ 1

$\frac{x }{\sqrt{x^6 + 5} } < \frac{x}{\sqrt{x^6} } =\frac{x}{x^3} = \frac{1}{x^2}$

$3) \displaystyle \int\limits^{+\infty}_1\dfrac{1}{x^2} \;dx , ~ p= 2 > 1$ ⇒сходится, а значит исходный интеграл тоже сходится

fctdgsygfdhngfxzgsac: Спасибо большое)

aa2517495: здравствуйте, можете помочь пожалуйста

polarkat: Не делайте ему, он просто переписывает, аналогичные задания кидает и всё

Новые вопросы

Литература, 9 месяцев назад

Алгебра, 9 месяцев назад

Алгебра, 11 месяцев назад

Українська література, 11 месяцев назад

Физика, 6 лет назад

Алгебра, 6 лет назад