даю 100 баллов геометрия

Ответы на вопрос
Ответ:
30°
Объяснение:
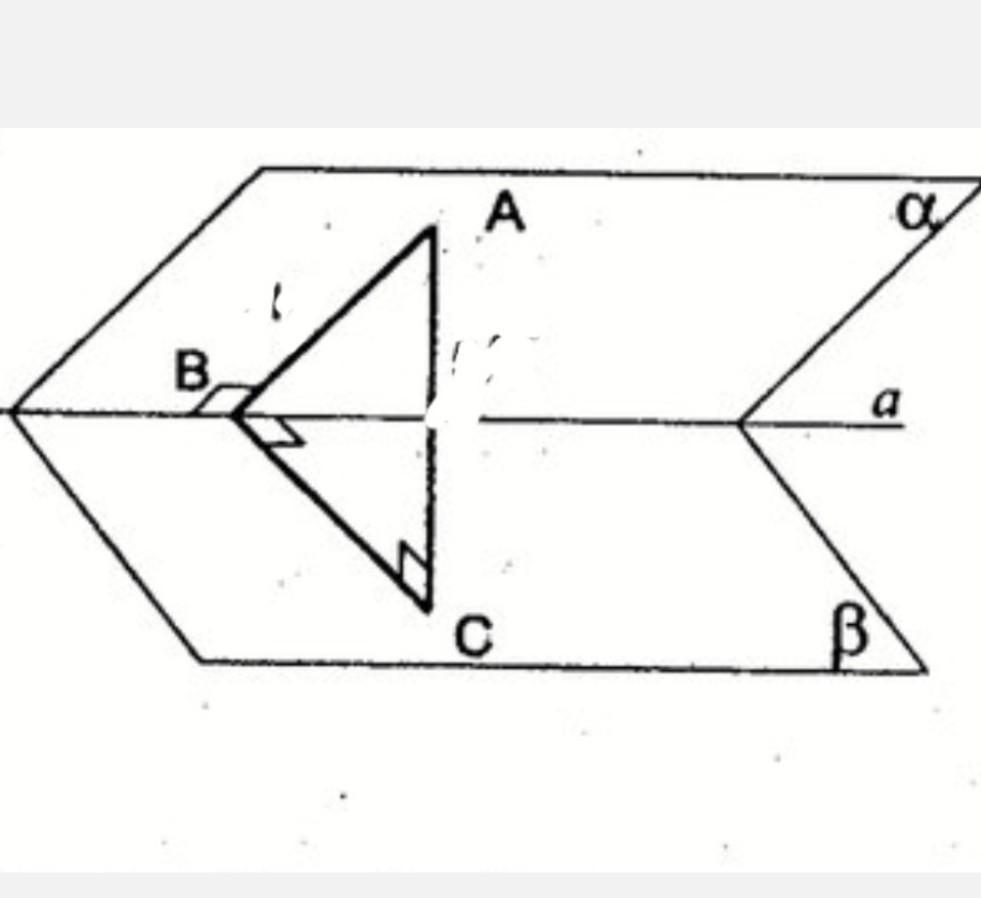
АС=4 см -перпендикуляр , опущенный на плоскость β,т.е расстояние от А до плоскости β.
АВ=8 см - перпендикуляр , опущенный на прямую а.
∆АВС - прямоугольный:
∠АВС -угол между плоскостями α и β
sin ∠ABC=BC/AB=4/8=1/2
∠ABC=30°
Ответ:
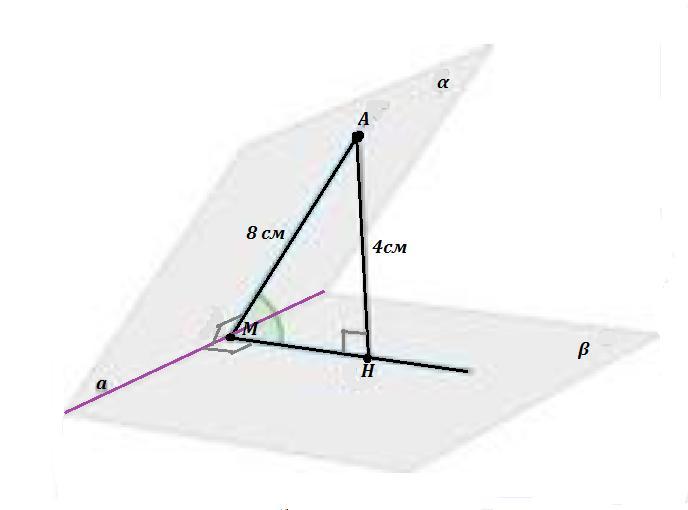
Точка А ∈ пл.α , α ∩ β = а .
Расстояние от точки А до прямой а равно длине перпендикуляра АМ , проведённого из точки А к прямой а в пл. α , АМ=8 см .
Расстояние от точки А до плоскости β - это длина перпендикуляра, проведённого из точки А к пл. β , то есть АН ⊥ пл.β , АН=4 см .
Угол между плоскостями α и β равен углу между прямой АМ и проекцией отрезка АМ на пл. β - отрезком МН .
ΔАМН - прямоугольный , ∠АНМ=90° , sin∠AМH=AH/AM = 4/8=1/2 .
Острый угол, синус которого равен 1/2, равен 30° .
∠АМН = 30°