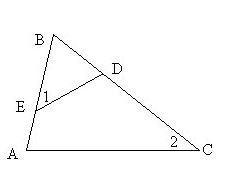
Дано, что AB = 10,2; БД = 3,4; ДК = 11,9. Расчитайте АЕ.

Не забудьте доказать подобие треугольников.

Ответ:

Чтобы решить AE в треугольнике ABE, нам сначала нужно доказать подобие треугольников ABE и ACD.

Дано:

АВ = 10,2

БД = 3,4

ДК = 11,9

Чтобы доказать подобие, мы можем использовать тот факт, что оба треугольника имеют общий угол и параллельные линии. В частности, если мы докажем, что угол AEB конгруэнтен углу ADC и прямые BE и CD-параллельны

Рассчитаем AE, доказав сходство:

1. Доказательство сходства

Угол AEB и угол ADC являются вертикальными углами и поэтому равны.

Прямые BE и CD параллельны, потому что BD — поперечная прямая и BC : DC = 3,4 : 11,9 = 1 : 3,4, что означает, что BE параллельна CD по теореме Фалеса.

2. Расчет AE

Если треугольники ABE и ACD подобны, мы можем составить пропорцию, исходя из соответствующих сторон:

AE/AB = AD/AC

AE/10.2 = AD/AD+DC

AE/10.2 = AD/AD+11.9

Учитывая AD = AB - BD = 10,2 - 3,4 = 6,8

AE/10.2 = 6.8/6.8+11.9

AE/10.2 = 6.8/18.7

AE = 10.2×6.8/18.7

AE ≈ 3.72

Следовательно, АЕ ≈ 3,72.

Объяснение: