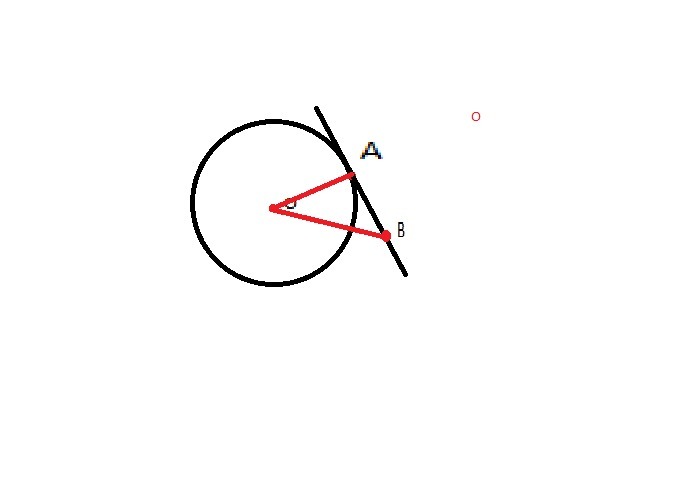
Через точку A, лежащую на поверхности шара, диаметр которого 10 см, проведена касательная плоскость. Найдите расстояние от центра шара до точки B, расположенной в плоскости так, что AB=12 см.

1. Т.к. диаметр = 10 = радиус = 5 ⇒ ОА = 5 см
2. По свойству касательной угол OBA = 90° = Треугольник OBA - прямоугольный
3. По теореме Пифагора OB² = AB² + AO²
OB² = 12² + 5²
OB² = 144 + 25
OB² = 169
OB = 13
Ответ: ОВ = 13 см

Пусть точка О-центр шара.Тогда радиус шара равен ОА=1/2*10=5см.Касательная перпендикулярна радиусу,проведенному в точку касания.Следовательно ОА_|_АВ.Получили прямоугольный треугольник,в котором катеты ОА=5см И АВ=12см
Гипотенузу ОВ найдем по теореме Пифагора
ОВ=√(ОА²+АВ²)=√(25+144)=√169=13см