БУДЬ ЛАСКА ДОПОМОЖІТЬ ДАЮ 100 БАЛЛІВ
До задачи необхідно виконувати рисунок, записувати коротку умову, повне та обгрунтоване розв’язання.

Сторони трикутника дорівнюють 13 см, 4 см та 15 см. Знайдіть косинус найменшого кута трикутника.

Ответ:

cos∠B= 63/65.

Объяснение:

Стороны треугольника равны 13 см, 4 см и 15 см. Найти косинус наименьшего угла.

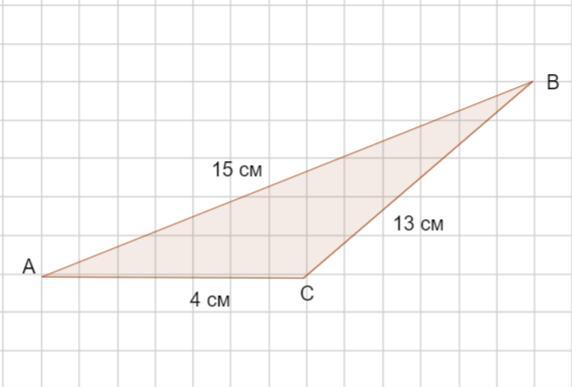
Дано: Δ АВС

АВ = 15 см

ВС = 13 см

АС = 4 см

Найти: косинус наименьшего угла.

Решение: Напротив наименьшей стороны в треугольнике лежит наименьший угол. Так как сторона АС = 4 см наименьшая, то ∠В - наименьший. Тогда надо найти cos ∠B.

Воспользуемся теоремой косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

AC² = AB² + BC² - 2·AB · BC ·cos∠B;

4² = 13² +15² - 2 · 13 · 15 ·cos∠B;

16= 169 +225 - 26· 15·cos∠B;

16= 394 -  390 · cos∠B;

390 ·cos∠B = 394 - 16;

390· cos∠ B = 378;

cos∠B = 378/ 390;

cos∠B= 126/ 130 ;

cos∠B= 63/65.

#SPJ1