Алгебра
Помогите решить

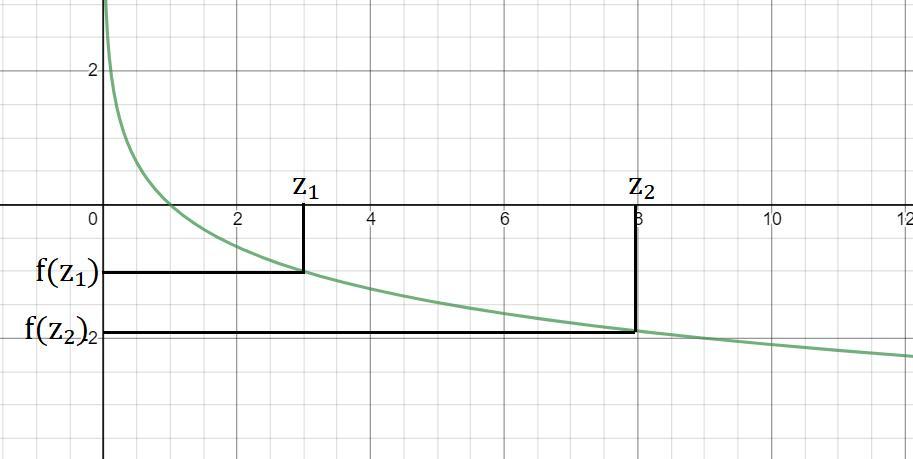
0 < 1/3 < 1, поэтому это убывающая функция, чем больше аргумент, тем меньше значение функции, на просят узнать когда значение ≤ другого значения, поэтому аргумент (x²+2x) ≥ 3 при условии ОДЗ выражения. Важно понимать, что так можно делать только потому, что функция всегда убывает и слева, и справа одна и та же функция . Это был просто комментарий, теперь продолжение решения.

Ответ: